Nem todas as estatísticas que nos são apresentadas podem ser analisadas e certificadas como dignas de credibilidade, como uma substância é analisada e certificada num laboratório de química. Huff [HUFF, Darrel, How to Lie with Statistics. New York: W W Norton & Company INC, 1954, pág. 122-142] sugere 5 perguntas que se forem feitas, podem ser facilmente respondidas e fornecem uma dica do que estamos vendo. Com isso podemos evitar aprender informações que na verdade não são bem assim.
1 Quem diz isso?
Huff [HUFF, Darrel, How to Lie with Statistics. New York: W W Norton & Company INC, 1954, pág. 123] explica: “O primeiro item a procurar é a tendência – o laboratório com alguma coisa a provar por causa de uma teoria, da reputação ou de um pagamento; o jornal cujo objetivo é uma boa história; trabalhadores e patrões com os níveis de salário em jogo”. Lembre-se que mesmo os laboratórios independentes podem ter interesses em jogo.
Geralmente essas estatísticas tendenciosas são caracterizadas por afirmações enganosas, ambíguas ou que não podem ser provadas; por seleção de dados favoráveis e supressão de desfavoráveis; unidades de medida faltando ou que mudam sem aviso; seleção de uma referência errada para comparação levando a um resultado que interesse mais; uso de parâmetros não especificados, como no caso da palavra “média” que é usada para cobrir os parâmetros de “mediana” e “moda” também, e é usada de acordo com o interesse do produtor.
2 Como ele sabe?
Questione como foi possível o produtor levantar estes dados. Muitas vezes os dados são de amostras tendenciosas, com indivíduos selecionados para que o resultado seja o esperado pelo produtor, ou que a amostragem é tão pequena que qualquer resultado poderia ser possível, mas somente aquele resultado que interessa ao produtor é publicado.
Pergunte-se: É a amostragem grande o suficiente para permitir qualquer conclusão confiável? É grande o suficiente para ter um significado?
Também desconfie de números com precisões injustificadas, que geralmente tendem a enganar simulando uma autoridade sem fundamento.
Ou ainda medições de valores difíceis de quantificar, como o nível de energia de uma pessoa, o desempenho sexual, ou a sensação de conforto. Para estas medições de aspectos humanos existem metodologias que garantem os melhores resultados possíveis; verifique se foi usada uma metodologia adequada, ou se o produtor baseou-se apenas na entrevista de algumas pessoas. E lembre-se que neste tipo de pesquisa o entrevistado também pode distorcer o resultado. São poucas as pessoas que se sentem à vontade para admitir que tenham disfunções sexuais, problemas psicológicos, ou até mau hálito.
3 O que está faltando?
O que está faltando é difícil identificar, mas fornece uma boa dica de como a estatística está sendo usada para confundir, ou de uma falha em seus argumentos. A ausência de algum parâmetro ou valor, particularmente se a fonte está interessada no resultado, é suficiente para jogar suspeita no argumento inteiro.
Procure por uma correlação fornecida sem uma medida de confiabilidade (erro provável, erro padrão), e será um indício de uma estatística não muito séria. Também procure por uma média de variedade não especificada, em qualquer assunto onde a média, a mediana e a moda podem diferir substancialmente.
4 Alguém mudou o assunto?
Huff [HUFF, Darrel, How to Lie with Statistics. New York: W W Norton & Company INC, 1954, pág. 131] em seu livro chama a atenção: “Quando avaliando uma estatística, procure por uma mudança em algum lugar entre os valores brutos e a conclusão. Um assunto é muitas vezes informado como outro”.
Geralmente isso ocorre pela assunção de uma correlação que não pode ser provada. A mudança de assunto ocorre quando se apresenta que algo “é devido a” algum motivo, formando uma conclusão sobre os dados. Mas essa relação é somente assumida como sendo verdadeira, e não pode ser provada.
É como no exemplo em que os dados estatísticos mostram que o número de casos registrados de uma determinada doença aumentou em relação à pesquisa anterior. Mas isso não necessariamente significa que a doença está se espalhando. Pode ter havido uma mudança nos critérios para registro dessa doença que aumentam o número de casos que são registrados, ou o aumento do conhecimento sobre a doença permite a identificação de casos quando antes não se sabia a causa; ou o sistema de saúde está cobrindo uma área maior com mais pessoas. Tudo isso pode explicar o aumento de casos registrados, sem significar, necessariamente, que a doença está se espalhando. Isso invalida a conclusão que a correlação entre o aumento de casos registrados e a disseminação da doença seja verdade. Os dados estatísticos mostram um aumento dos casos registrados, e só; ela não mostra um aumento nos casos da doença, embora possa sugerir isso; a correlação ficou por conta da imaginação, desatenção ou desonestidade do produtor da informação.
A mudança de assunto ocorre quando presumimos que algo significa automaticamente outro. Correlação não implica causação, mas é somente um indício que ela pode existir.
Essa correlação “forçada” é especialmente estimulada quando temos estatísticas que não se ajustam completamente bem ao propósito que queremos, então correlacionamos o que queremos saber com os dados que temos. Como no exemplo anterior, a estatística dos casos registrados da doença foi utilizada para estimar o número de casos da doença, podendo levar a uma conclusão errônea sobre o alastramento de uma epidemia, mesmo que os números da estatística estejam corretos. No entanto, muitas vezes esses são os melhores números que podemos conseguir, e o produtor tem que julgar por si mesmo se eles são realmente apropriados para o fim desejado, e se for o caso informar adequadamente o consumidor da informação das premissas utilizadas para a correlação.
5 Isso faz sentido?
Uma pergunta simples, que requer somente um pouco de exercício da imaginação para ser respondida, e, no entanto pode evitar conclusões gravemente erradas.
A pergunta “isso faz sentido?” provoca uma análise objetiva que muitas vezes irá derrubar uma estatística baseada em assunções erradas, pelo simples motivo de elas não apresentarem uma coerência básica ou fugirem do bom senso, o que geralmente pode ser notado desde o princípio. Estatísticas com erros desse tipo só conseguem sucesso quando a aura mágica dos números causa uma suspensão do bom senso. Exemplos são as correlações absurdas, amostras claramente tendenciosas e fortes interesses do produtor.
Um outro exemplo de absurdo é a extrapolação incontrolada. Quando fazemos previsões baseadas em tendências do passado, ignoramos que para isso ocorrer está implícito que tudo o mais deverá estar igual e que a tendência tem que continuar a ocorrer. Mas no mundo real, por algum motivo o ambiente que nos cerca se recusa a permanecer igual, o que, aliás, se não ocorresse faria a vida ser muito chata.
Um aumento grande e constante no passado, não significa necessariamente que o aumento continuará a ocorrer na mesma velocidade, pois o mercado fica saturado com produtos, as pessoas chegam ao seu limite de consumo em determinada área, o crescimento das famílias chega a um limite, o crescimento populacional esbarra em limitações naturais e de infra-estrutura, assim como a economia, entre outros.
sexta-feira, 29 de maio de 2009
QUESTIONE AS ESTATÍSTICAS
quinta-feira, 28 de maio de 2009
CITAÇÃO INCITADORA - PARTE 7
“Existem três tipos de mentiras: mentiras, mentiras abomináveis, e estatísticas”.
- Bejamin Disraeli, político e escritor britânico (1804-1881)
quarta-feira, 27 de maio de 2009
ENTENDA MAIS AS ESTATÍSTICAS - PARTE 3
Um exemplo de termo vago muito usado é várias vezes citado por Huff [HUFF, Darrel, How to Lie with Statistics. New York: W W Norton & Company INC, 1954, pág. 28] em seu livro. Ele descreve o uso enganoso que pode-se fazer da palavra “média”: “Um truque comum é usar a palavra ‘média’ para diferentes tipos de média, pois este termo é bem vago. Este é um truque comumente usado, algumas vezes inocentemente mas geralmente intencionalmente, por pessoas querendo influenciar a opinião pública ou vender espaços de publicidade. Quando te dizem que alguma coisa é uma média você não sabe muito sobre isso até que possa descobrir quais dos tipos comuns de média é – média, mediana ou moda”.
A figura abaixo, preparada por Huff, é uma ótima ilustração das diferenças entre média, mediana e moda. Neste caso, é a análise estatística do salário dos trabalhadores em uma fábrica.
Usar somente a “média” como um argumento estatístico pode ser um indício de estatística tendenciosa, principalmente se a média não for especificada. Huff [HUFF, Darrel, How to Lie with Statistics. New York: W W Norton & Company INC, 1954, pág. 42 e 43] escreve: “Geralmente uma média – seja ela uma média, mediana, especificada ou não – é de tal simplificação excessiva que é pior do que inútil. Saber nada sobre o assunto é freqüentemente mais saudável que saber o que não é, e um pequeno aprendizado pode ser uma condição perigosa”.
E também há o erro estatístico, que é uma estimativa do erro entre o que foi observado e o valor que se espera confirmar. É como nas pesquisas de intenção de voto nas eleições, em que é informado que o erro da pesquisa pode levar os resultados 2% ou 3% para cima ou para baixo. Este valor é importante quando comparamos valores semelhantes, pois, se considerado o erro estatístico, as conclusões sobre o quadro geral podem ser diferentes, como o resultado esperado de uma eleição ou a comparação dos resultados de um teste. Lembre-se que comparações entre valores com diferenças pequenas só têm significado se você manter em mente este mais-ou-menos, mesmo (ou especialmente) quando isso não é informado.
Desconfie de estatísticas com resultados muito precisos. Cerca de 93,2151734% de todas as estatísticas alegam uma precisão de resultados que não pode ser justificada pelo método empregado. Na afirmação anterior parece óbvio que tal precisão não passa de uma piada. Mas num momento de desatenção ou de leitura sem crítica, não é difícil creditarmos como verdadeiras as estatísticas que “estimam” que 40,87% das intenções de voto são para determinado candidato, que uma pasta de dente é 23,19% mais eficiente em evitar cáries que as concorrentes, ou que um energético aumenta o nível de energia em 32,82%. Como eles podem saber disso, com essa precisão? Quais métodos foram empregados? Estes métodos justificam a divulgação de números com tal resolução? Tais resoluções geralmente advêm de cálculos matemáticos, usados para calcular médias ou outro parâmetro qualquer, mas não provam e nem indicam a precisão do método estatístico utilizado. O problema é que números arredondados parecem falsos, e até certo grau são mesmo, mas na maioria dos casos são mais que suficiente para informar, com o devido grau de precisão que a estatística oferece, e são mais fáceis de lembrar e comparar. Mas números muito precisos geralmente impressionam muito as pessoas, e por isso são muito usados.
Outro tipo de informação cuja ausência pode levar a desentendimentos, é aquela que diz a faixa ou amplitude da amostra ou o seu desvio da média, este último geralmente representado pelo desvio-padrão.
As estatísticas na maioria das vezes se concentram nas médias, em torno de um ponto central. O interesse na maioria dos casos é com o que ocorre no corpo principal dos resultados, no que é freqüente, normal e mediano. No entanto, algumas vezes são os extremos que nos interessam, é aquilo que se afasta ao máximo do ponto central, tanto em uma das extremidades quanto em outra. É o que ocorre com quem quer determinar o peso máximo que uma ponte deve suportar, ou identificar o ponto fraco em um sistema.
Como no exemplo da minha falha em compreender as estatísticas de expectativa de vida, se fosse informado as idades máximas, eu não teria incorrido no mesmo erro. Um monte de confusão pode ser evitado se à média for acrescentada uma indicação da faixa de variação.
terça-feira, 26 de maio de 2009
CITAÇÃO INCITADORA - PARTE 6
“Primeiro consiga os seus fatos; então os distorça ao seu bel prazer”.
- Mark Twain, escritor americano (1835-1910)
segunda-feira, 25 de maio de 2009
ENTENDA MAIS AS ESTATÍSTICAS - PARTE 2
Um portador comum de erros e mentiras é a amostragem. A amostragem vai determinar a qualidade dos resultados estatísticos. Não são raros os casos de estudos ou pesquisas que tiram conclusões baseadas em amostras pequenas, que fornecem resultados pouco sólidos. Quanto maior a amostragem, menores são os erros estatísticos. Huff [HUFF, Darrel, How to Lie with Statistics. New York: W W Norton & Company INC, 1954, pág. 13] afirma que “o procedimento de amostragem é o coração de grande parte das estatísticas que você encontra sobre todo tipo de assunto”.
Mas os truques mais desonestos com a amostragem são aqueles que selecionam os dados mais convenientes para os cálculos dos parâmetros estatísticos, o que é agravado pelas facilidades oferecidas pelo computador. Agora é fácil escolher entre dezenas de combinações de dados, gráficos e testes estatísticos, e selecionar para a publicação aqueles que melhor defendem o ponto de vista do produtor. Esta seleção de dados é conhecida como “mineração dos dados”, e é parecida com as técnicas dos mágicos, que escolhem o que revelar e o que esconder para manter a atenção do iludido público. O consumidor deve sempre considerar que provavelmente o que está sendo mostrado são os dados minerados, ou a combinação de dados que melhor serve aos propósitos do produtor.
E não se deixe enganar pela terminologia; muitas vezes índices e estatísticas têm o mesmo nome, mas isso não significa que são equivalentes, e nem que podem ser colocadas lado a lado e serem comparadas. Muitas vezes elas vêm de contextos totalmente diferentes, e apresentam critérios e cálculos distintos. É o caso de estatísticas realizadas por órgãos governamentais, que levam em consideração o contexto de seus próprios países, e geralmente não podem ser diretamente comparados com os mesmo índices de outros países.
Como exemplo, o índice de desemprego pesquisado e calculado pelo governo da Alemanha para seu país, pode ser incomparável ao índice de desemprego estimado pelo governo brasileiro; são países com contextos totalmente diferentes, e os critérios para considerar uma pessoa desempregada podem ser diferentes, como com relação ao tempo sem emprego necessário para ser considerada desempregada, a consideração sobre os trabalhos autônomos, outras fontes de renda que não de um emprego, situação de emprego do cônjuge, se está procurando trabalho ou não, entre outros. Para o governo dos EUA, por exemplo, pessoas sem emprego, mas que estão ativamente procurando por trabalho, não são consideradas desempregadas.
sexta-feira, 22 de maio de 2009
ENTENDA MAIS AS ESTATÍSTICAS - PARTE 1
Tome como exemplo o conjunto de dados abaixo. Eles são um conjunto de números aleatórios, entre 0 e 1, bastante adequados para este exemplo por sua simplicidade, mas que poderiam ser substituídos por qualquer outro conjunto de números.
Olhando para este conjunto de números não conseguimos tirar nenhuma conclusão; eles parecem somente um emaranhado de números com três casas decimais, sem significado.
O número mais alto é 0,996. O número mais baixo é 0,009. Agora sabemos a faixa que estes dados abrangem.
A média aritmética, que é a soma de todos os números divididos pela quantidade de números, é 0,458. A sua mediana, que é o número central, ou seja, apresenta a mesma quantidade de números com valores menores e valores maiores, é 0,461. Note que essas duas médias têm valores muito parecidos, típico das distribuições naturais, como a altura de pessoas, as notas das provas em uma sala de aula ou os níveis de colesterol em determinada população, e também para as distribuições aleatórias, como essa.
A moda é 0,140, que é o número que ocorre com mais freqüência, aparecendo 3 vezes.
O percentil de 25% é 0,192, ou seja, o conjunto de 25% dos números com valores mais baixos está abaixo desse valor. O percentil de 75% é 0,697, ou seja, os 75% dos números com valores mais baixos estão abaixo de desse valor.
O desvio-padrão é ±0,288. Ele é uma medida da dispersão dos dados em torno da média aritmética, quando a distribuição segue a curva no formato de um sino, típica das distribuições naturais. Ele é apresentado como um valor positivo e negativo (±) em torno da média. Esta medida significa que 33% dos números da amostra estão dentro de uma faixa de 0,288 abaixo da média, e outros 33% estão dentro de uma faixa de 0,288 acima da média.
Então podemos sumarizar o conjunto de dados acima nos seguintes parâmetros estatísticos:
- Valor máximo: 0,996
- Valor mínimo: 0,009
- Média aritmética: 0,458
- Mediana: 0,461
- Moda: 0,140
- Percentil de 25%; 0,192
- Percentil de 75%; 0,697
- Desvio-padrão: ±0,288
E quanto mais parâmetros estatísticos usarmos, melhor e mais clara será a representação daquele conjunto de dados. Se tivéssemos apresentado somente a média aritmética, o que é bem comum nas estatísticas por aí, teríamos uma visão muito mais deficiente do conjunto de dados. À medida que adicionamos novos parâmetros, que podem ser muitos outros além dos que foram apresentados acima, podemos formar uma visão mais clara do todo.
Mas não se engane. Os parâmetros estatísticos podem esconder erros graves. As médias, relações, tendências e gráficos não são sempre o que parecem; podem esconder alguma informação ou mostrar o que não existe.
quinta-feira, 21 de maio de 2009
CITAÇÃO INCITADORA - PARTE 5
“Pensamento estatístico será um dia tão necessário para uma cidadania eficiente como a habilidade de ler e escrever”.
- H. G. Wells, escritor britânico (1866-1946)
quarta-feira, 20 de maio de 2009
MENTALIDADE ESTATÍSTICA - PARTE 2
A maioria das pessoas não estudou muito estatística, e nem têm grande facilidade para matemática mais complexa. No entanto têm a impressão errada de que são necessários muitos conhecimentos avançados de matemática para entender análises estatísticas. As pessoas nem chegam a considerar entender estatística, por considerá-la acima de suas capacidades de compreensão.
Mas para compreender a maioria das aplicações da estatística, principalmente na mídia, um conhecimento básico é suficiente. Qualquer pessoa pode facilmente adquirir uma “mentalidade estatística”, compreendendo o significado de alguns termos, como média, mediana, moda, desvio-padrão, curva normal, probabilidades, erro padrão da média, erro provável, amplitude total, correlação, universo de amostragem, erros de amostragem, limite de segurança entre outros. Com isso poderá compreender os resultados das estatísticas, mesmo que nunca tenha aprendido a executar qualquer um dos cálculos de estatística.
O livro “How to Lie With Statistics” [HUFF, Darrel, How to Lie with Statistics, 1954] (“Como mentir com estatísticas”), Darrel Huff explica conceitos básicos de estatística em um texto leve, curto e agradável de ler, com ilustrações engraçadas. Apresenta muitos exemplos de situações reais em que as estatísticas foram usadas para enganar, confundir, ou simplesmente foram mal feitos ou sofreram de erros comuns, sempre levando a conclusões enganosas ou imprecisas.
Escrito por um jornalista autônomo, que não tinha nenhuma especialização em estatística, este livro é um exemplo de como se pode adquirir uma “mentalidade estatística”, ao mesmo tempo em que não se precisa recorrer a mais do que a álgebra básica e a conceitos fáceis de compreender.
Não é à toa (ou por uma ironia, visto que o autor não é um estatístico) que este livro é considerado o texto sobre estatística mais lido no mundo. Escrito em 1954, mas com temas ainda perfeitamente atuais, o livro já vendeu mais de 1,5 milhões de cópias na sua edição em inglês.
Nele, Huff [HUFF, Darrel, How to Lie with Statistics. New York: W W Norton & Company INC, 1954, pág. 8] afirma: “A linguagem secreta das estatísticas, tão atraente em uma cultura voltada a fatos, é empregada para sensacionalizar, inflar, confundir, e simplificar em excesso. Métodos estatísticos e termos estatísticos são necessários para relatar a massa de dados das tendências sociais e econômicas, condições de negócios, pesquisas de ‘opinião’, e o censo. Mas sem escritores que usem as palavras com honestidade e entendimento e leitores que saibam o que elas significam, o resultado só pode ser um absurdo semântico”.
Mas muitas pessoas não se interessam por estudar estatística, por terem dela um conhecimento intuitivo e que acreditam suficientes. Mas saber como as estatísticas são calculadas nos permite entender o que seus resultados realmente significam e nos permite experimentar uma sensação de posse do que está sendo informado.
terça-feira, 19 de maio de 2009
CITAÇÃO INCITADORA - PARTE 4
“Um conhecimento de estatísticas é como o conhecimento de línguas estrangeiras ou de álgebra; ela pode se provar útil a qualquer hora e sob qualquer circunstância”.
- Arthur Lyon Bowley, economista e estatístico britânico (1869-1957)
segunda-feira, 18 de maio de 2009
MENTALIDADE ESTATÍSTICA - PARTE 1
Compreender as aplicações da análise estatística é um dos conhecimentos mais úteis na Era da Compreensão. São inúmeras as ocasiões em que esta habilidade pode salvar o consumidor de informações de armadilhas, ou evitar que o produtor engane o consumidor por pura ignorância ou falta de atenção. E também é uma habilidade necessária para compreender o mundo a nossa volta e exercer plenamente a nossa cidadania.
Quando eu era criança li que a expectativa de vida média a partir do momento do nascimento durante o Império Romano era de 28 anos; logo, imaginei que as pessoas morriam por volta dessa idade, e me perguntava como era a vida de pessoas que sabiam que iam morrer tão jovens. Li também que a expectativa de vida média no mundo no final do século XIX era de 37 anos, e que a atual é de cerca de 67 anos. Como as pessoas passaram a viver em média 30 anos a mais em apenas um século? Será que houve mudanças genéticas em nós ao longo da história recente que nos fizeram viver mais? Essas dúvidas me pareciam bem incoerentes.
Não, não houve mudanças genéticas recentes que nos fizeram ter vidas mais longas. As pessoas na época do Império Romano eram capazes de viver tanto tempo quanto as pessoas de hoje; é só conferir a idade a que chegaram poetas, filósofos, artistas ou políticos romanos ou gregos, que morreram de causas naturais, e não por doenças ou assassinatos.
A partir do momento que compreendi que essas estatísticas de expectativa de vida não refletiam uma média da longevidade do ser humano, e sim a média do tempo de vida de uma determinada população, as dúvidas desapareceram.
A evolução dos números nas estatísticas de expectativa de vida deve-se à forma como ela é calculada. Ela considera qualquer tipo de morte, por acidente, assassinato, doenças, guerras, e o mais importante, as mortes dos recém nascidos e crianças, cujas taxas são altas em sociedades pouco desenvolvidas, como as sociedades antigas. Conforme o mundo foi se desenvolvendo, curas para doenças foram criadas e as condições de vida melhoraram, resultando entre outros numa queda acentuada da mortalidade infantil, e assim aumentando a expectativa de vida média quando considerada a partir do momento do nascimento; no entanto as pessoas que conseguem sobreviver às causas de morte não naturais continuam morrendo com idade avançada, como há 2.000 anos.
Depois de toda essa confusão e de descobrir como esta estatística é calculada e o que ela realmente significa, pude adquirir uma mentalidade estatística sobre este assunto. Agora sei que se em um país havia dois habitantes, e um morreu com 99 anos, e o outro apenas com apenas 1 ano de idade, a expectativa de vida média desse país será a simples média aritmética das idades de morte, ou seja, de 50 anos. Essa média tem uma grande diferença para os valores de suas parcelas, e por isso pode-se dizer que é uma estatística com dispersão alta.
Em algumas sociedades pouco desenvolvidas, para evitar que as altas taxas de mortalidade infantil distorçam essas estatísticas, a média de vida é calculada a partir dos 5 anos de idade, ao invés do momento do nascimento. E isso me parece óbvio e correto agora, que entendo como a estatística de vida é calculada. Da próxima vez que eu ver uma média da expectativa de vida, vou questionar se ela é a partir do nascimento ou a partir dos 5 anos de idade.
Nós nos deixamos influenciar por informações numéricas, e não as questionamos, o que nos impede de compreendê-las realmente. Então o mais provável é que sejamos enganados. Assim, é melhor ignorar uma informação que não se entende, do que tentar agir baseado nela.
sábado, 16 de maio de 2009
CITAÇÃO INCITADORA - PARTE 3
“Nunca se mente tanto como antes das eleições, durante uma guerra e depois de uma caçada”.
- Otto von Bismarck, estadista alemão (1815-1898)
sexta-feira, 15 de maio de 2009
ESTATÍSTICAS NA MÍDIA, NA PUBLICIDADE E EM ESTUDOS
Estatísticas são usadas extensivamente na mídia, na publicidade e em todos os tipos de estudo. Não somente porque os números são capazes de informar de uma maneira que as palavras não conseguem, ou sumarizar uma grande massa de dados em uma só afirmação, mas também porque eles podem ser facilmente manipulados e expressos da maneira que for mais conveniente, defendendo qualquer ponto de vista, e, contudo, sem você estar tecnicamente mentindo. Você não pode provar qualquer fato com estatísticas, mas pode sempre encontrar algo bom ou mal para dizer sobre o assunto.
Estamos atolados por números e estatísticas que nos atingem por todos os lados, afirmando verdades e gritando por uma importância que não questionamos, por acreditar que se eles estão lá, devem estar corretos e devem ser importantes para nós. São tantas estatísticas querendo provar todo tipo de fatos, que muitas até mesmo se contradizem.
Raramente questionamos estes números por considerarmos que se eles estão lá, são corretos e válidos, ou pelo menos alguém já teve o trabalho de verificá-los. Mas isto muitas vezes não é verdade; não passa de informação falsa ou simplesmente não-informação. Números que são publicados sem qualquer referência ou verificação podem induzir as pessoas a ações e comportamentos prejudiciais.
Mesmo números que sempre acreditamos serem de suma importância, como os índices das bolsas de valores, como o IBOVESPA, por exemplo, são só a média de um conjunto de ações de grandes empresas, e não representam o mercado de ações como um todo.
A publicidade é um campo em que sempre temos que questionar o interesse da fonte da informação sobre o que está sendo afirmado. Mesmo nos casos em que estatísticas e avaliações são creditadas a laboratórios independentes, possivelmente os números certos foram escolhidos com um propósito ou algumas informações foram omitidas para transmitir a mensagem certa.
Não é difícil se deparar com comerciais em revistas, jornais, televisão, rádio, Internet ou até em e-mails spams patrocinados por fontes suspeitas, afirmações do tipo (todas elas são apenas exemplos fantasiosos, mas relembram bastante as publicidades que estão por aí):
“Aveia ajuda a baixar as taxas de colesterol em 35% dos casos”, em um estudo de um laboratório “independente” patrocinado por uma indústria de cereais.
“Chocolates ajudam a evitar cáries”, uma descoberta creditada a uma marca de chocolates.
“Tomar café diariamente ajuda a melhorar a memória em 22%”, em pesquisa de uma associação de produtores de café.
“Tomar café diariamente aumenta em 67% as chances de ter gastrite”, em pesquisa de uma associação de produtores de leite.
“Tomar vinho tinto todos os dias aumenta em 5 anos a expectativa de vida”, associação de vinícolas.
“Esse novo espremedor de laranja tira 28% a mais de suco que os outros”, na caixa do eletrodoméstico sendo vendido no supermercado.
“Comer peixe 4 vezes por semana diminui em 58% a chance de um ataque cardíaco”, associação dos comerciantes de peixe.
“Leite de cabra do Himalaia aumenta o nível de potência sexual masculina em 86% depois de 3 meses de uso diário”, importadores de leite de cabra do Himalaia.
Os mais desatentos podem não perceber, mas em todas essas afirmações aparentemente claras, sucintas e diretas ao ponto, estão sérios problemas de manipulação de números e omissão de dados importantes, além é claro, do óbvio interesse do produtor na divulgação dessas informações.
O interesse do produtor geralmente está em exagerar alguma nuance de seus dados estatísticos, para corroborar a sua opinião ou ponto de vista. É o que mais comumente acontece nos meios noticiosos, que tendem a exagerar os quadros que as estatísticas sugerem para tornar as matérias e reportagens mais interessantes e conseqüentemente mais vendáveis. E é difícil acreditar que essas distorções são motivadas por pura ignorância ou preguiça, e que não há uma dose de culpa do produtor, pois quase sempre as situações são exageradas, e quase nunca minimizadas.
Esses produtores de informação esperam que você engula qualquer ponto de vista baseado em números escolhidos a dedo e em estatísticas infundadas. Como Huff [HUFF, Darrel, How to Lie with Statistics. New York: W W Norton & Company INC, 1954, pág. 47] explica: “Parece que o repórter passou pra frente algumas palavras sem se questionar o que elas significam, e espera-se que você as leia tão sem crítica quanto eles para a feliz ilusão que elas te dão de ter aprendido algo. Isto tudo é remanescente de uma velha definição de método de lecionamento da instrução na sala de aula: o processo pelo qual o conteúdo de um livro de texto do instrutor é transferido para o caderno de notas do estudante sem passar através das cabeças de nenhum dos dois”. Mas não é assim com quem tem uma mentalidade estatística.
quinta-feira, 14 de maio de 2009
CITAÇÃO INCITADORA - PARTE 2
- Joseph Stalin, estadista soviético (1878-1953)
quarta-feira, 13 de maio de 2009
INTRODUÇÃO - ESTATÍSTICAS
A partir de hoje este blog mudará o seu foco. Até agora o foco foram os gráficos. Mas como o texto de "Sobre" deste blog explica, o assunto também envolve estatísticas!
Afinal, é mais fácil ainda mentir sutilmente com estatísticas, pois não há pistas visuais que podem levar o leitor a descobrir o que está errado; com as estatísticas, fica tudo mais abstrato.
Sendo assim, incia-se aqui a segunda parte, que tratará das estatísticas. As postagens sobre estatísticas poderão parecer um pouco mais "pesadas", com textos mais longos e sem muitas figuras, o que pode tornar o assunto menos atrativo para alguns. No entanto, tentarei ao máximo manter o assunto o mais "leve" e interessante possível.
Espero que gostem!
Alessandro
segunda-feira, 11 de maio de 2009
BARRAS INDIGESTAS - CASO 10
As barras repousam sobre um eixo que sobe da esquerda para a direita, fazendo com que as barras da direita terminem em alturas relativamente superiores que as suas vizinhas da esquerda, passando a impressão para o leitor distraído que houve um aumento de produção maior que o ocorrido. Note como a barra de 2002 termina em uma altura muito superior que a barra de 1999, sugerindo um aumento de cerca de 50%, enquanto na verdade houve um aumento de menos de 30% em relação à produção de 1999. Pelo menos há várias linhas da escala vertical que cortam o plano de fundo do gráfico, e ajudam o leitor a manter o rumo enquanto compara as barras, mitigando as distorções que a representação de profundidade está causando. Se a projeção em 2D tivesse sido adotada, essas linhas seriam dispensáveis, diminuindo os elementos gráficos que não trazem informação, ou se preferir, o “lixo de gráfico”.
Gráfico do relatório anual de um grande estatal brasileira, mostrando a evolução do volume de produção. O uso desnecessário de uma perspectiva em 3D novamente distorce as relações e engana o leitor. Neste caso poderia sugerir um aumento de produção maior que o indicado pelos números.
sexta-feira, 8 de maio de 2009
BARRAS INDIGESTAS - CASO 9
quarta-feira, 6 de maio de 2009
EVOLUÇÕES RETRÓGRADAS - CASO 1
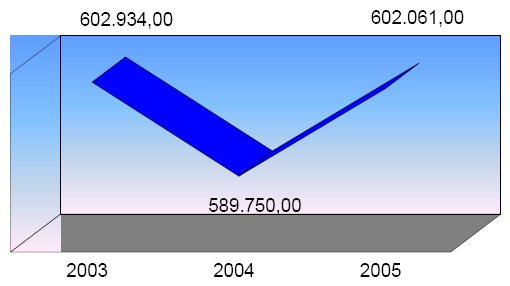
O gráfico abaixo transforma uma linha num plano quando adiciona a dimensão de profundidade, o que não traz informação nova, mas apenas confusão. É esperado do leitor que ele acompanhe a linha formada pela parte da frente ou de trás do plano?
Além disso, a escala vertical não começa no zero, aumentando a percepção da variação. Se colocada numa escala de base zero, o gráfico mostraria quase uma constante.
Este gráfico apresenta apenas seis números (três anos, e três valores), e ocupa uma área considerável do relatório. É um exemplo de representação de dados de baixíssima densidade. Poucas publicações têm uma densidade de dados por centímetro quadrado tão baixo como este gráfico. Seria muito melhor ter usado uma tabela, que ocuparia uma fração do espaço e realizaria o mesmo trabalho.
segunda-feira, 4 de maio de 2009
BARRAS INDIGESTAS - CASO 8
O gráfico a seguir apresenta dois problemas. O primeiro problema é que a escala não começa no zero, um assunto que já foi discutido. O outro problema é que a face de trás das barras é mais alta que a face da frente. O produtor do gráfico espera que eu leia o valor da barra pela altura de qual das faces? Para a barra mais à esquerda, a face frontal indica cerca de 17,8, e a de trás indica 18. Pelo menos o produtor teve o cuidado de colocar rotulações diretas sobre cada barra, indicando os seus valores. Este recurso ameniza o problema da perspectiva errada, no entanto não elimina o problema das barras inutilmente representadas em 3D.
Infelizmente as barras em 3D estão cada vez mais populares nos ambientes corporativos e gerentes estão realmente tomando decisões operacionais e estratégicas baseados neste tipo de gráfico. É assustador.
sexta-feira, 1 de maio de 2009
TORTAS AZEDAS - CASO 5
O gráfico está distorcido, mas de forma irregular. Não é possível concluir se o gráfico está inclinado para a esquerda, direita, ou se está em forma ovalada. A espessura da rosca parece variar também. Este gráfico é quase um desenho projetado para causar ilusão de ótica. A fatia da região Sudeste que é indicada com 56,2%, no gráfico parece contar com menos da metade da área, enquanto os 5,4% da região Norte parecem maior que o devido.