Download do livro "Informação é Prata, Compreensão é Ouro"

Caros Leitores,
É com muita satisfação que disponibilizo o livro "Informação é Prata, Compreensão é Ouro - Um guia para todos sobre como produzir e consumir informação na Era da Compreensão".

 

O livro pode ser baixado gratuitamente à partir do link abaixo, e distribuído livremente.

http://www.archive.org/details/InformacaoEPrataCompreensoEOuro

 

Esta é a única obra escrita em português sobre a importância da compreensão na tão famosa “Era da Informação”, abordando temas como o déficit de atenção, o analfabetismo funcional no Brasil, sobrecarga e ansiedade de informação, arquitetura da informação, problemas das pessoas comuns com gráficos e estatísticas enganosos, o uso de e-mail e outros meios de comunicação digital, e as limitações do uso de programas de slideware em apresentações, numa abordagem voltada para a realidade brasileira. Realizei uma revisão bibliográfica inédita, concentrando os ensinamentos das maiores autoridades em cada área pesquisada e ligando os seus ensinamentos num texto conciso e voltado ao seu objetivo: mostrar a importância de compreender na sociedade da informação.

Trata de um assunto extremamente atual, muito divulgado nos EUA e que ainda não é discutido seriamente no Brasil. Aqui, a sobrecarga e a ansiedade de informação, a importância da compreensão e outros temas relacionados são conhecidos pelas pessoas, que até usam estes termos no seu cotidiano para diagnosticar situações problemáticas, mas sem maiores conhecimentos ou qualquer pista de como superá-las. Neste livro, estes assuntos são abordados de forma fácil de entender, contando com o uso de várias imagens e figuras.

Público-alvo: Profissionais liberais, executivos, empresários, trabalhadores autônomos, funcionários públicos, estudantes de ensino médio, estudantes universitários. Usuários da Internet, leitores de livros, jornais e revistas, usuários de equipamentos eletrônicos de comunicação, apresentadores em reuniões. Leitores que gostam de ler sobre desenvolvimento pessoal e profissional, novas tendências tecnológicas e suas implicações na vida cotidiana.

-->Este trabalho está disponibilizado como emailware. Isto significa que não há custo para o leitor desde que o trabalho seja utilizado nas condições descritas na Licença "Creative Commons" descrita nele. O único pedido que o emailware faz é que o leitor que gostou deste trabalho envie um e-mail para o autor (para compreensaoeouro@gmail.com) com suas sugestões, comentários, críticas ou elogios. É uma forma rápida e barata de demonstrar apreço pelo trabalho de outras pessoas.

Espero que gostem! Aproveitem e divulguem, pois é informação útil e gratuita! 

Obrigado,
Alessandro Nicoli de Mattos

QUESTIONE AS ESTATÍSTICAS

Nem todas as estatísticas que nos são apresentadas podem ser analisadas e certificadas como dignas de credibilidade, como uma substância é analisada e certificada num laboratório de química. Huff [HUFF, Darrel, How to Lie with Statistics. New York: W W Norton & Company INC, 1954, pág. 122-142] sugere 5 perguntas que se forem feitas, podem ser facilmente respondidas e fornecem uma dica do que estamos vendo. Com isso podemos evitar aprender informações que na verdade não são bem assim.

1 Quem diz isso?

Huff [HUFF, Darrel, How to Lie with Statistics. New York: W W Norton & Company INC, 1954, pág. 123] explica: “O primeiro item a procurar é a tendência – o laboratório com alguma coisa a provar por causa de uma teoria, da reputação ou de um pagamento; o jornal cujo objetivo é uma boa história; trabalhadores e patrões com os níveis de salário em jogo”. Lembre-se que mesmo os laboratórios independentes podem ter interesses em jogo.

Geralmente essas estatísticas tendenciosas são caracterizadas por afirmações enganosas, ambíguas ou que não podem ser provadas; por seleção de dados favoráveis e supressão de desfavoráveis; unidades de medida faltando ou que mudam sem aviso; seleção de uma referência errada para comparação levando a um resultado que interesse mais; uso de parâmetros não especificados, como no caso da palavra “média” que é usada para cobrir os parâmetros de “mediana” e “moda” também, e é usada de acordo com o interesse do produtor.

2 Como ele sabe?

Questione como foi possível o produtor levantar estes dados. Muitas vezes os dados são de amostras tendenciosas, com indivíduos selecionados para que o resultado seja o esperado pelo produtor, ou que a amostragem é tão pequena que qualquer resultado poderia ser possível, mas somente aquele resultado que interessa ao produtor é publicado.

Pergunte-se: É a amostragem grande o suficiente para permitir qualquer conclusão confiável? É grande o suficiente para ter um significado?

Também desconfie de números com precisões injustificadas, que geralmente tendem a enganar simulando uma autoridade sem fundamento.

Ou ainda medições de valores difíceis de quantificar, como o nível de energia de uma pessoa, o desempenho sexual, ou a sensação de conforto. Para estas medições de aspectos humanos existem metodologias que garantem os melhores resultados possíveis; verifique se foi usada uma metodologia adequada, ou se o produtor baseou-se apenas na entrevista de algumas pessoas. E lembre-se que neste tipo de pesquisa o entrevistado também pode distorcer o resultado. São poucas as pessoas que se sentem à vontade para admitir que tenham disfunções sexuais, problemas psicológicos, ou até mau hálito.

3 O que está faltando?

O que está faltando é difícil identificar, mas fornece uma boa dica de como a estatística está sendo usada para confundir, ou de uma falha em seus argumentos. A ausência de algum parâmetro ou valor, particularmente se a fonte está interessada no resultado, é suficiente para jogar suspeita no argumento inteiro.

Procure por uma correlação fornecida sem uma medida de confiabilidade (erro provável, erro padrão), e será um indício de uma estatística não muito séria. Também procure por uma média de variedade não especificada, em qualquer assunto onde a média, a mediana e a moda podem diferir substancialmente.

4 Alguém mudou o assunto?

Huff [HUFF, Darrel, How to Lie with Statistics. New York: W W Norton & Company INC, 1954, pág. 131] em seu livro chama a atenção: “Quando avaliando uma estatística, procure por uma mudança em algum lugar entre os valores brutos e a conclusão. Um assunto é muitas vezes informado como outro”.

Geralmente isso ocorre pela assunção de uma correlação que não pode ser provada. A mudança de assunto ocorre quando se apresenta que algo “é devido a” algum motivo, formando uma conclusão sobre os dados. Mas essa relação é somente assumida como sendo verdadeira, e não pode ser provada.

É como no exemplo em que os dados estatísticos mostram que o número de casos registrados de uma determinada doença aumentou em relação à pesquisa anterior. Mas isso não necessariamente significa que a doença está se espalhando. Pode ter havido uma mudança nos critérios para registro dessa doença que aumentam o número de casos que são registrados, ou o aumento do conhecimento sobre a doença permite a identificação de casos quando antes não se sabia a causa; ou o sistema de saúde está cobrindo uma área maior com mais pessoas. Tudo isso pode explicar o aumento de casos registrados, sem significar, necessariamente, que a doença está se espalhando. Isso invalida a conclusão que a correlação entre o aumento de casos registrados e a disseminação da doença seja verdade. Os dados estatísticos mostram um aumento dos casos registrados, e só; ela não mostra um aumento nos casos da doença, embora possa sugerir isso; a correlação ficou por conta da imaginação, desatenção ou desonestidade do produtor da informação.

A mudança de assunto ocorre quando presumimos que algo significa automaticamente outro. Correlação não implica causação, mas é somente um indício que ela pode existir.

Essa correlação “forçada” é especialmente estimulada quando temos estatísticas que não se ajustam completamente bem ao propósito que queremos, então correlacionamos o que queremos saber com os dados que temos. Como no exemplo anterior, a estatística dos casos registrados da doença foi utilizada para estimar o número de casos da doença, podendo levar a uma conclusão errônea sobre o alastramento de uma epidemia, mesmo que os números da estatística estejam corretos. No entanto, muitas vezes esses são os melhores números que podemos conseguir, e o produtor tem que julgar por si mesmo se eles são realmente apropriados para o fim desejado, e se for o caso informar adequadamente o consumidor da informação das premissas utilizadas para a correlação.

5 Isso faz sentido?

Uma pergunta simples, que requer somente um pouco de exercício da imaginação para ser respondida, e, no entanto pode evitar conclusões gravemente erradas.

A pergunta “isso faz sentido?” provoca uma análise objetiva que muitas vezes irá derrubar uma estatística baseada em assunções erradas, pelo simples motivo de elas não apresentarem uma coerência básica ou fugirem do bom senso, o que geralmente pode ser notado desde o princípio. Estatísticas com erros desse tipo só conseguem sucesso quando a aura mágica dos números causa uma suspensão do bom senso. Exemplos são as correlações absurdas, amostras claramente tendenciosas e fortes interesses do produtor.

Um outro exemplo de absurdo é a extrapolação incontrolada. Quando fazemos previsões baseadas em tendências do passado, ignoramos que para isso ocorrer está implícito que tudo o mais deverá estar igual e que a tendência tem que continuar a ocorrer. Mas no mundo real, por algum motivo o ambiente que nos cerca se recusa a permanecer igual, o que, aliás, se não ocorresse faria a vida ser muito chata.

Um aumento grande e constante no passado, não significa necessariamente que o aumento continuará a ocorrer na mesma velocidade, pois o mercado fica saturado com produtos, as pessoas chegam ao seu limite de consumo em determinada área, o crescimento das famílias chega a um limite, o crescimento populacional esbarra em limitações naturais e de infra-estrutura, assim como a economia, entre outros.

CITAÇÃO INCITADORA - PARTE 7

“Existem três tipos de mentiras: mentiras, mentiras abomináveis, e estatísticas”.

- Bejamin Disraeli, político e escritor britânico (1804-1881)

ENTENDA MAIS AS ESTATÍSTICAS - PARTE 3

Outro problema comum é o uso de termos vagos, que podem se aplicar a mais de um parâmetro estatístico, e que podem ser escolhidos de acordo com a conveniência do produtor. Sempre questione a definição das medidas que são usadas naquela estatística em particular.

Um exemplo de termo vago muito usado é várias vezes citado por Huff [HUFF, Darrel, How to Lie with Statistics. New York: W W Norton & Company INC, 1954, pág. 28] em seu livro. Ele descreve o uso enganoso que pode-se fazer da palavra “média”: “Um truque comum é usar a palavra ‘média’ para diferentes tipos de média, pois este termo é bem vago. Este é um truque comumente usado, algumas vezes inocentemente mas geralmente intencionalmente, por pessoas querendo influenciar a opinião pública ou vender espaços de publicidade. Quando te dizem que alguma coisa é uma média você não sabe muito sobre isso até que possa descobrir quais dos tipos comuns de média é – média, mediana ou moda”.

A figura abaixo, preparada por Huff, é uma ótima ilustração das diferenças entre média, mediana e moda. Neste caso, é a análise estatística do salário dos trabalhadores em uma fábrica.

Figura tirada de “A Produção de Informações Estratégicas”, de Platt, que foi adaptada do livro “How to Lie with Statistics”, de Huff. Uma ótima lustração das diferenças entre média, mediana e moda. [PLATT, Washington. A Produção de Informações Estratégicas. Rio de Janeiro: Agir Editora, 1974. Figura da pág. 225]

Note que neste caso, as diferenças entre os 3 tipos de média são bem acentuadas, e cada média pode se prestar a defender um tipo diferente de argumento. Os sindicalistas podem usar a mediana ou a moda como “média” para defender que a maioria dos trabalhadores ganha pouco e merece um aumento. Enquanto que os patrões podem usar a média aritmética, que é a mais alta devido à influência dos altos salários de uns poucos funcionários da liderança, para defender que a “média” de salários na fábrica é alta e que reajustes salariais não são necessários.

Usar somente a “média” como um argumento estatístico pode ser um indício de estatística tendenciosa, principalmente se a média não for especificada. Huff [HUFF, Darrel, How to Lie with Statistics. New York: W W Norton & Company INC, 1954, pág. 42 e 43] escreve: “Geralmente uma média – seja ela uma média, mediana, especificada ou não – é de tal simplificação excessiva que é pior do que inútil. Saber nada sobre o assunto é freqüentemente mais saudável que saber o que não é, e um pequeno aprendizado pode ser uma condição perigosa”.

E também há o erro estatístico, que é uma estimativa do erro entre o que foi observado e o valor que se espera confirmar. É como nas pesquisas de intenção de voto nas eleições, em que é informado que o erro da pesquisa pode levar os resultados 2% ou 3% para cima ou para baixo. Este valor é importante quando comparamos valores semelhantes, pois, se considerado o erro estatístico, as conclusões sobre o quadro geral podem ser diferentes, como o resultado esperado de uma eleição ou a comparação dos resultados de um teste. Lembre-se que comparações entre valores com diferenças pequenas só têm significado se você manter em mente este mais-ou-menos, mesmo (ou especialmente) quando isso não é informado.

Desconfie de estatísticas com resultados muito precisos. Cerca de 93,2151734% de todas as estatísticas alegam uma precisão de resultados que não pode ser justificada pelo método empregado. Na afirmação anterior parece óbvio que tal precisão não passa de uma piada. Mas num momento de desatenção ou de leitura sem crítica, não é difícil creditarmos como verdadeiras as estatísticas que “estimam” que 40,87% das intenções de voto são para determinado candidato, que uma pasta de dente é 23,19% mais eficiente em evitar cáries que as concorrentes, ou que um energético aumenta o nível de energia em 32,82%. Como eles podem saber disso, com essa precisão? Quais métodos foram empregados? Estes métodos justificam a divulgação de números com tal resolução? Tais resoluções geralmente advêm de cálculos matemáticos, usados para calcular médias ou outro parâmetro qualquer, mas não provam e nem indicam a precisão do método estatístico utilizado. O problema é que números arredondados parecem falsos, e até certo grau são mesmo, mas na maioria dos casos são mais que suficiente para informar, com o devido grau de precisão que a estatística oferece, e são mais fáceis de lembrar e comparar. Mas números muito precisos geralmente impressionam muito as pessoas, e por isso são muito usados.

Outro tipo de informação cuja ausência pode levar a desentendimentos, é aquela que diz a faixa ou amplitude da amostra ou o seu desvio da média, este último geralmente representado pelo desvio-padrão.

As estatísticas na maioria das vezes se concentram nas médias, em torno de um ponto central. O interesse na maioria dos casos é com o que ocorre no corpo principal dos resultados, no que é freqüente, normal e mediano. No entanto, algumas vezes são os extremos que nos interessam, é aquilo que se afasta ao máximo do ponto central, tanto em uma das extremidades quanto em outra. É o que ocorre com quem quer determinar o peso máximo que uma ponte deve suportar, ou identificar o ponto fraco em um sistema.

Como no exemplo da minha falha em compreender as estatísticas de expectativa de vida, se fosse informado as idades máximas, eu não teria incorrido no mesmo erro. Um monte de confusão pode ser evitado se à média for acrescentada uma indicação da faixa de variação.

CITAÇÃO INCITADORA - PARTE 6

“Primeiro consiga os seus fatos; então os distorça ao seu bel prazer”.

- Mark Twain, escritor americano (1835-1910)

ENTENDA MAIS AS ESTATÍSTICAS - PARTE 2

Um portador comum de erros e mentiras é a amostragem. A amostragem vai determinar a qualidade dos resultados estatísticos. Não são raros os casos de estudos ou pesquisas que tiram conclusões baseadas em amostras pequenas, que fornecem resultados pouco sólidos. Quanto maior a amostragem, menores são os erros estatísticos. Huff [HUFF, Darrel, How to Lie with Statistics. New York: W W Norton & Company INC, 1954, pág. 13] afirma que “o procedimento de amostragem é o coração de grande parte das estatísticas que você encontra sobre todo tipo de assunto”.

Mas os truques mais desonestos com a amostragem são aqueles que selecionam os dados mais convenientes para os cálculos dos parâmetros estatísticos, o que é agravado pelas facilidades oferecidas pelo computador. Agora é fácil escolher entre dezenas de combinações de dados, gráficos e testes estatísticos, e selecionar para a publicação aqueles que melhor defendem o ponto de vista do produtor. Esta seleção de dados é conhecida como “mineração dos dados”, e é parecida com as técnicas dos mágicos, que escolhem o que revelar e o que esconder para manter a atenção do iludido público. O consumidor deve sempre considerar que provavelmente o que está sendo mostrado são os dados minerados, ou a combinação de dados que melhor serve aos propósitos do produtor.

E não se deixe enganar pela terminologia; muitas vezes índices e estatísticas têm o mesmo nome, mas isso não significa que são equivalentes, e nem que podem ser colocadas lado a lado e serem comparadas. Muitas vezes elas vêm de contextos totalmente diferentes, e apresentam critérios e cálculos distintos. É o caso de estatísticas realizadas por órgãos governamentais, que levam em consideração o contexto de seus próprios países, e geralmente não podem ser diretamente comparados com os mesmo índices de outros países.

Como exemplo, o índice de desemprego pesquisado e calculado pelo governo da Alemanha para seu país, pode ser incomparável ao índice de desemprego estimado pelo governo brasileiro; são países com contextos totalmente diferentes, e os critérios para considerar uma pessoa desempregada podem ser diferentes, como com relação ao tempo sem emprego necessário para ser considerada desempregada, a consideração sobre os trabalhos autônomos, outras fontes de renda que não de um emprego, situação de emprego do cônjuge, se está procurando trabalho ou não, entre outros. Para o governo dos EUA, por exemplo, pessoas sem emprego, mas que estão ativamente procurando por trabalho, não são consideradas desempregadas.

ENTENDA MAIS AS ESTATÍSTICAS - PARTE 1

Ao estudar um grande volume de dados, muitas vezes as únicas conclusões valiosas são aquelas fornecidas pela estatística, por seus parâmetros como o desvio-padrão, média, mediana ou moda, por exemplo. Quando se deve consumir uma grande massa de dados, a tarefa é muito difícil sem um parâmetro sumarizador.

Tome como exemplo o conjunto de dados abaixo. Eles são um conjunto de números aleatórios, entre 0 e 1, bastante adequados para este exemplo por sua simplicidade, mas que poderiam ser substituídos por qualquer outro conjunto de números.

Olhando para este conjunto de números não conseguimos tirar nenhuma conclusão; eles parecem somente um emaranhado de números com três casas decimais, sem significado.

No entanto, podemos reduzir este conjunto de dados a alguns parâmetros estatísticos, que nos fornecem informações sumarizantes:

O número mais alto é 0,996. O número mais baixo é 0,009. Agora sabemos a faixa que estes dados abrangem.

A média aritmética, que é a soma de todos os números divididos pela quantidade de números, é 0,458. A sua mediana, que é o número central, ou seja, apresenta a mesma quantidade de números com valores menores e valores maiores, é 0,461. Note que essas duas médias têm valores muito parecidos, típico das distribuições naturais, como a altura de pessoas, as notas das provas em uma sala de aula ou os níveis de colesterol em determinada população, e também para as distribuições aleatórias, como essa.

A moda é 0,140, que é o número que ocorre com mais freqüência, aparecendo 3 vezes.

O percentil de 25% é 0,192, ou seja, o conjunto de 25% dos números com valores mais baixos está abaixo desse valor. O percentil de 75% é 0,697, ou seja, os 75% dos números com valores mais baixos estão abaixo de desse valor.

O desvio-padrão é ±0,288. Ele é uma medida da dispersão dos dados em torno da média aritmética, quando a distribuição segue a curva no formato de um sino, típica das distribuições naturais. Ele é apresentado como um valor positivo e negativo (±) em torno da média. Esta medida significa que 33% dos números da amostra estão dentro de uma faixa de 0,288 abaixo da média, e outros 33% estão dentro de uma faixa de 0,288 acima da média.

Então podemos sumarizar o conjunto de dados acima nos seguintes parâmetros estatísticos:

• Valor máximo: 0,996
• Valor mínimo: 0,009
• Média aritmética: 0,458
• Mediana: 0,461
• Moda: 0,140
• Percentil de 25%; 0,192
• Percentil de 75%; 0,697
• Desvio-padrão: ±0,288

Estes parâmetros nos fornecem uma boa síntese do conjunto de dados acima, da qual podemos tirar conclusões; é claro que não têm a mesma precisão e nem substituem o conjunto de dados, mas fornecem uma boa dica do que ele é.

E quanto mais parâmetros estatísticos usarmos, melhor e mais clara será a representação daquele conjunto de dados. Se tivéssemos apresentado somente a média aritmética, o que é bem comum nas estatísticas por aí, teríamos uma visão muito mais deficiente do conjunto de dados. À medida que adicionamos novos parâmetros, que podem ser muitos outros além dos que foram apresentados acima, podemos formar uma visão mais clara do todo.

Mas não se engane. Os parâmetros estatísticos podem esconder erros graves. As médias, relações, tendências e gráficos não são sempre o que parecem; podem esconder alguma informação ou mostrar o que não existe.

CITAÇÃO INCITADORA - PARTE 5

“Pensamento estatístico será um dia tão necessário para uma cidadania eficiente como a habilidade de ler e escrever”.

- H. G. Wells, escritor britânico (1866-1946)

MENTALIDADE ESTATÍSTICA - PARTE 2

A maioria das pessoas não estudou muito estatística, e nem têm grande facilidade para matemática mais complexa. No entanto têm a impressão errada de que são necessários muitos conhecimentos avançados de matemática para entender análises estatísticas. As pessoas nem chegam a considerar entender estatística, por considerá-la acima de suas capacidades de compreensão.

Mas para compreender a maioria das aplicações da estatística, principalmente na mídia, um conhecimento básico é suficiente. Qualquer pessoa pode facilmente adquirir uma “mentalidade estatística”, compreendendo o significado de alguns termos, como média, mediana, moda, desvio-padrão, curva normal, probabilidades, erro padrão da média, erro provável, amplitude total, correlação, universo de amostragem, erros de amostragem, limite de segurança entre outros. Com isso poderá compreender os resultados das estatísticas, mesmo que nunca tenha aprendido a executar qualquer um dos cálculos de estatística.

O livro “How to Lie With Statistics” [HUFF, Darrel, How to Lie with Statistics, 1954] (“Como mentir com estatísticas”), Darrel Huff explica conceitos básicos de estatística em um texto leve, curto e agradável de ler, com ilustrações engraçadas. Apresenta muitos exemplos de situações reais em que as estatísticas foram usadas para enganar, confundir, ou simplesmente foram mal feitos ou sofreram de erros comuns, sempre levando a conclusões enganosas ou imprecisas.

Escrito por um jornalista autônomo, que não tinha nenhuma especialização em estatística, este livro é um exemplo de como se pode adquirir uma “mentalidade estatística”, ao mesmo tempo em que não se precisa recorrer a mais do que a álgebra básica e a conceitos fáceis de compreender.

Não é à toa (ou por uma ironia, visto que o autor não é um estatístico) que este livro é considerado o texto sobre estatística mais lido no mundo. Escrito em 1954, mas com temas ainda perfeitamente atuais, o livro já vendeu mais de 1,5 milhões de cópias na sua edição em inglês.

Nele, Huff [HUFF, Darrel, How to Lie with Statistics. New York: W W Norton & Company INC, 1954, pág. 8] afirma: “A linguagem secreta das estatísticas, tão atraente em uma cultura voltada a fatos, é empregada para sensacionalizar, inflar, confundir, e simplificar em excesso. Métodos estatísticos e termos estatísticos são necessários para relatar a massa de dados das tendências sociais e econômicas, condições de negócios, pesquisas de ‘opinião’, e o censo. Mas sem escritores que usem as palavras com honestidade e entendimento e leitores que saibam o que elas significam, o resultado só pode ser um absurdo semântico”.

Mas muitas pessoas não se interessam por estudar estatística, por terem dela um conhecimento intuitivo e que acreditam suficientes. Mas saber como as estatísticas são calculadas nos permite entender o que seus resultados realmente significam e nos permite experimentar uma sensação de posse do que está sendo informado.

CITAÇÃO INCITADORA - PARTE 4

“Um conhecimento de estatísticas é como o conhecimento de línguas estrangeiras ou de álgebra; ela pode se provar útil a qualquer hora e sob qualquer circunstância”.

- Arthur Lyon Bowley, economista e estatístico britânico (1869-1957)

MENTALIDADE ESTATÍSTICA - PARTE 1

Compreender as aplicações da análise estatística é um dos conhecimentos mais úteis na Era da Compreensão. São inúmeras as ocasiões em que esta habilidade pode salvar o consumidor de informações de armadilhas, ou evitar que o produtor engane o consumidor por pura ignorância ou falta de atenção. E também é uma habilidade necessária para compreender o mundo a nossa volta e exercer plenamente a nossa cidadania.

Quando eu era criança li que a expectativa de vida média a partir do momento do nascimento durante o Império Romano era de 28 anos; logo, imaginei que as pessoas morriam por volta dessa idade, e me perguntava como era a vida de pessoas que sabiam que iam morrer tão jovens. Li também que a expectativa de vida média no mundo no final do século XIX era de 37 anos, e que a atual é de cerca de 67 anos. Como as pessoas passaram a viver em média 30 anos a mais em apenas um século? Será que houve mudanças genéticas em nós ao longo da história recente que nos fizeram viver mais? Essas dúvidas me pareciam bem incoerentes.

Não, não houve mudanças genéticas recentes que nos fizeram ter vidas mais longas. As pessoas na época do Império Romano eram capazes de viver tanto tempo quanto as pessoas de hoje; é só conferir a idade a que chegaram poetas, filósofos, artistas ou políticos romanos ou gregos, que morreram de causas naturais, e não por doenças ou assassinatos.

A partir do momento que compreendi que essas estatísticas de expectativa de vida não refletiam uma média da longevidade do ser humano, e sim a média do tempo de vida de uma determinada população, as dúvidas desapareceram.

A evolução dos números nas estatísticas de expectativa de vida deve-se à forma como ela é calculada. Ela considera qualquer tipo de morte, por acidente, assassinato, doenças, guerras, e o mais importante, as mortes dos recém nascidos e crianças, cujas taxas são altas em sociedades pouco desenvolvidas, como as sociedades antigas. Conforme o mundo foi se desenvolvendo, curas para doenças foram criadas e as condições de vida melhoraram, resultando entre outros numa queda acentuada da mortalidade infantil, e assim aumentando a expectativa de vida média quando considerada a partir do momento do nascimento; no entanto as pessoas que conseguem sobreviver às causas de morte não naturais continuam morrendo com idade avançada, como há 2.000 anos.

Depois de toda essa confusão e de descobrir como esta estatística é calculada e o que ela realmente significa, pude adquirir uma mentalidade estatística sobre este assunto. Agora sei que se em um país havia dois habitantes, e um morreu com 99 anos, e o outro apenas com apenas 1 ano de idade, a expectativa de vida média desse país será a simples média aritmética das idades de morte, ou seja, de 50 anos. Essa média tem uma grande diferença para os valores de suas parcelas, e por isso pode-se dizer que é uma estatística com dispersão alta.

Em algumas sociedades pouco desenvolvidas, para evitar que as altas taxas de mortalidade infantil distorçam essas estatísticas, a média de vida é calculada a partir dos 5 anos de idade, ao invés do momento do nascimento. E isso me parece óbvio e correto agora, que entendo como a estatística de vida é calculada. Da próxima vez que eu ver uma média da expectativa de vida, vou questionar se ela é a partir do nascimento ou a partir dos 5 anos de idade.

Nós nos deixamos influenciar por informações numéricas, e não as questionamos, o que nos impede de compreendê-las realmente. Então o mais provável é que sejamos enganados. Assim, é melhor ignorar uma informação que não se entende, do que tentar agir baseado nela.

CITAÇÃO INCITADORA - PARTE 3

“Nunca se mente tanto como antes das eleições, durante uma guerra e depois de uma caçada”.

- Otto von Bismarck, estadista alemão (1815-1898)

ESTATÍSTICAS NA MÍDIA, NA PUBLICIDADE E EM ESTUDOS

Estatísticas são usadas extensivamente na mídia, na publicidade e em todos os tipos de estudo. Não somente porque os números são capazes de informar de uma maneira que as palavras não conseguem, ou sumarizar uma grande massa de dados em uma só afirmação, mas também porque eles podem ser facilmente manipulados e expressos da maneira que for mais conveniente, defendendo qualquer ponto de vista, e, contudo, sem você estar tecnicamente mentindo. Você não pode provar qualquer fato com estatísticas, mas pode sempre encontrar algo bom ou mal para dizer sobre o assunto.

Estamos atolados por números e estatísticas que nos atingem por todos os lados, afirmando verdades e gritando por uma importância que não questionamos, por acreditar que se eles estão lá, devem estar corretos e devem ser importantes para nós. São tantas estatísticas querendo provar todo tipo de fatos, que muitas até mesmo se contradizem.

Raramente questionamos estes números por considerarmos que se eles estão lá, são corretos e válidos, ou pelo menos alguém já teve o trabalho de verificá-los. Mas isto muitas vezes não é verdade; não passa de informação falsa ou simplesmente não-informação. Números que são publicados sem qualquer referência ou verificação podem induzir as pessoas a ações e comportamentos prejudiciais.

Mesmo números que sempre acreditamos serem de suma importância, como os índices das bolsas de valores, como o IBOVESPA, por exemplo, são só a média de um conjunto de ações de grandes empresas, e não representam o mercado de ações como um todo.

A publicidade é um campo em que sempre temos que questionar o interesse da fonte da informação sobre o que está sendo afirmado. Mesmo nos casos em que estatísticas e avaliações são creditadas a laboratórios independentes, possivelmente os números certos foram escolhidos com um propósito ou algumas informações foram omitidas para transmitir a mensagem certa.

Não é difícil se deparar com comerciais em revistas, jornais, televisão, rádio, Internet ou até em e-mails spams patrocinados por fontes suspeitas, afirmações do tipo (todas elas são apenas exemplos fantasiosos, mas relembram bastante as publicidades que estão por aí):

“Aveia ajuda a baixar as taxas de colesterol em 35% dos casos”, em um estudo de um laboratório “independente” patrocinado por uma indústria de cereais.
“Chocolates ajudam a evitar cáries”, uma descoberta creditada a uma marca de chocolates.
“Tomar café diariamente ajuda a melhorar a memória em 22%”, em pesquisa de uma associação de produtores de café.
“Tomar café diariamente aumenta em 67% as chances de ter gastrite”, em pesquisa de uma associação de produtores de leite.
“Tomar vinho tinto todos os dias aumenta em 5 anos a expectativa de vida”, associação de vinícolas.
“Esse novo espremedor de laranja tira 28% a mais de suco que os outros”, na caixa do eletrodoméstico sendo vendido no supermercado.
“Comer peixe 4 vezes por semana diminui em 58% a chance de um ataque cardíaco”, associação dos comerciantes de peixe.
“Leite de cabra do Himalaia aumenta o nível de potência sexual masculina em 86% depois de 3 meses de uso diário”, importadores de leite de cabra do Himalaia.

Os mais desatentos podem não perceber, mas em todas essas afirmações aparentemente claras, sucintas e diretas ao ponto, estão sérios problemas de manipulação de números e omissão de dados importantes, além é claro, do óbvio interesse do produtor na divulgação dessas informações.

O interesse do produtor geralmente está em exagerar alguma nuance de seus dados estatísticos, para corroborar a sua opinião ou ponto de vista. É o que mais comumente acontece nos meios noticiosos, que tendem a exagerar os quadros que as estatísticas sugerem para tornar as matérias e reportagens mais interessantes e conseqüentemente mais vendáveis. E é difícil acreditar que essas distorções são motivadas por pura ignorância ou preguiça, e que não há uma dose de culpa do produtor, pois quase sempre as situações são exageradas, e quase nunca minimizadas.

Esses produtores de informação esperam que você engula qualquer ponto de vista baseado em números escolhidos a dedo e em estatísticas infundadas. Como Huff [HUFF, Darrel, How to Lie with Statistics. New York: W W Norton & Company INC, 1954, pág. 47] explica: “Parece que o repórter passou pra frente algumas palavras sem se questionar o que elas significam, e espera-se que você as leia tão sem crítica quanto eles para a feliz ilusão que elas te dão de ter aprendido algo. Isto tudo é remanescente de uma velha definição de método de lecionamento da instrução na sala de aula: o processo pelo qual o conteúdo de um livro de texto do instrutor é transferido para o caderno de notas do estudante sem passar através das cabeças de nenhum dos dois”. Mas não é assim com quem tem uma mentalidade estatística.

CITAÇÃO INCITADORA - PARTE 2

“Quando você mata um é uma tragédia, quando você mata dez milhões é uma estatística”.

- Joseph Stalin, estadista soviético (1878-1953)

INTRODUÇÃO - ESTATÍSTICAS

Caros Leitores,

A partir de hoje este blog mudará o seu foco. Até agora o foco foram os gráficos. Mas como o texto de "Sobre" deste blog explica, o assunto também envolve estatísticas!

Afinal, é mais fácil ainda mentir sutilmente com estatísticas, pois não há pistas visuais que podem levar o leitor a descobrir o que está errado; com as estatísticas, fica tudo mais abstrato.

Sendo assim, incia-se aqui a segunda parte, que tratará das estatísticas. As postagens sobre estatísticas poderão parecer um pouco mais "pesadas", com textos mais longos e sem muitas figuras, o que pode tornar o assunto menos atrativo para alguns. No entanto, tentarei ao máximo manter o assunto o mais "leve" e interessante possível.

Espero que gostem!

Alessandro

BARRAS INDIGESTAS - CASO 10

O gráfico de barras a seguir, retirado do relatório anual de uma grande empresa estatal brasileira, mostra a evolução do volume de produção. Novamente o uso desnecessário da perspectiva em 3D distorce o gráfico, lançando suspeitas sobre as intenções do produtor. Só porque os computadores têm capacidade para produzir tais gráficos, não significa que devemos testar os seus limites e produzir gráficos tão elaborados, quando um gráfico tradicional iria ser bem mais adequado.

As barras repousam sobre um eixo que sobe da esquerda para a direita, fazendo com que as barras da direita terminem em alturas relativamente superiores que as suas vizinhas da esquerda, passando a impressão para o leitor distraído que houve um aumento de produção maior que o ocorrido. Note como a barra de 2002 termina em uma altura muito superior que a barra de 1999, sugerindo um aumento de cerca de 50%, enquanto na verdade houve um aumento de menos de 30% em relação à produção de 1999. Pelo menos há várias linhas da escala vertical que cortam o plano de fundo do gráfico, e ajudam o leitor a manter o rumo enquanto compara as barras, mitigando as distorções que a representação de profundidade está causando. Se a projeção em 2D tivesse sido adotada, essas linhas seriam dispensáveis, diminuindo os elementos gráficos que não trazem informação, ou se preferir, o “lixo de gráfico”.

Gráfico do relatório anual de um grande estatal brasileira, mostrando a evolução do volume de produção. O uso desnecessário de uma perspectiva em 3D novamente distorce as relações e engana o leitor. Neste caso poderia sugerir um aumento de produção maior que o indicado pelos números.

BARRAS INDIGESTAS - CASO 9

Caso você ainda não esteja satisfeito com a aparência do seu gráfico de barras em 3D, você pode adicionar texturas de tijolos às barras, e fazê-las parecerem torres ou colunas que foram erguidas tijolo a tijolo. Talvez o produtor queria fazer uma metáfora do esforço necessário para alcançar tais resultados com o esforço de erguer tal construção.

Gráfico retirado do relatório anual da administradora de um porto brasileiro. Texturas foram adicionadas às barras para dar a aparência de sólidas construções. Mais um exemplo de “lixo de gráfico”.

Essas texturas, emaranhados de linhas e pontos, confundem e fazem doer os olhos do observador, além de poluírem visualmente o gráfico. São elementos gráficos que não adicionam informação nova, e por isso são mais um exemplo de “lixo de gráfico”.

EVOLUÇÕES RETRÓGRADAS - CASO 1

A ânsia por criar gráficos em três dimensões é tão grande que não se contenta com gráficos circulares transformados em tortas flutuantes ou em rodas. É também necessário dar profundidade à linha de um gráfico de evolução, que teoricamente não tem profundidade.

O gráfico abaixo transforma uma linha num plano quando adiciona a dimensão de profundidade, o que não traz informação nova, mas apenas confusão. É esperado do leitor que ele acompanhe a linha formada pela parte da frente ou de trás do plano?

Além disso, a escala vertical não começa no zero, aumentando a percepção da variação. Se colocada numa escala de base zero, o gráfico mostraria quase uma constante.

Este gráfico apresenta apenas seis números (três anos, e três valores), e ocupa uma área considerável do relatório. É um exemplo de representação de dados de baixíssima densidade. Poucas publicações têm uma densidade de dados por centímetro quadrado tão baixo como este gráfico. Seria muito melhor ter usado uma tabela, que ocuparia uma fração do espaço e realizaria o mesmo trabalho.

Gráfico do relatório de um programa social do governo brasileiro, mostrando a evolução dos recursos aplicados. Um gráfico de evolução espaçoso e em 3D para representar apenas seis números. Uma tabela teria realizado o mesmo trabalho ocupando apenas uma fração do espaço deste gráfico.

BARRAS INDIGESTAS - CASO 8

Geralmente não há uma regra para escolher a perspectiva em gráficos 3D. Um truque usado em gráficos de barras 3D é escolher uma perspectiva que faça a face de trás da barra estar num nível mais alto que a face da frente. Então o observador não sabe se o que deve ser comparado com a escala é a face da frente ou a de trás, que é mais alta e por isso representa um valor maior. Outros truques de perspectiva podem esconder as faces laterais ou criar outras relações entre a face frontal e traseira.

O gráfico a seguir apresenta dois problemas. O primeiro problema é que a escala não começa no zero, um assunto que já foi discutido. O outro problema é que a face de trás das barras é mais alta que a face da frente. O produtor do gráfico espera que eu leia o valor da barra pela altura de qual das faces? Para a barra mais à esquerda, a face frontal indica cerca de 17,8, e a de trás indica 18. Pelo menos o produtor teve o cuidado de colocar rotulações diretas sobre cada barra, indicando os seus valores. Este recurso ameniza o problema da perspectiva errada, no entanto não elimina o problema das barras inutilmente representadas em 3D.

Gráfico do relatório de um órgão governamental europeu, com barras tridimensionais cuja perspectiva deixam a face de trás mais alta que as da frente. Qual das faces indica o valor correto?

Se o uso de um gráfico de barras em 3D for realmente imprescindível, certifique-se de que a perspectiva deixe a face da frente mais alta, para não enfatizar a face traseira e confundir o observador quanto ao valor. Se necessário indique o valor de cada barra com um número no topo, como neste caso. Mas a melhor escolha continua sendo um gráfico em 2D, que economiza todo esse trabalho.

Infelizmente as barras em 3D estão cada vez mais populares nos ambientes corporativos e gerentes estão realmente tomando decisões operacionais e estratégicas baseados neste tipo de gráfico. É assustador.

TORTAS AZEDAS - CASO 5

O gráfico de rosca a seguir mostra a distribuição das vendas entre as regiões brasileiras de uma estatal brasileira. É um exemplo de gráfico que poderia ser perfeitamente projetado em uma perspectiva em 2D, mas a preocupação com o estilo e de fazer o relatório anual parecer legal e moderno, fez com que se escolhesse a representação em 3D, que somente distorce o gráfico.

O gráfico está distorcido, mas de forma irregular. Não é possível concluir se o gráfico está inclinado para a esquerda, direita, ou se está em forma ovalada. A espessura da rosca parece variar também. Este gráfico é quase um desenho projetado para causar ilusão de ótica. A fatia da região Sudeste que é indicada com 56,2%, no gráfico parece contar com menos da metade da área, enquanto os 5,4% da região Norte parecem maior que o devido.

Gráfico do relatório anual de uma estatal brasileira, mostrando a distribuição das vendas entre as regiões do Brasil. Outro exemplo de como o desnecessário uso da perspectiva em 3D deforma os gráficos.

TORTAS AZEDAS - CASO 4

O gráfico de torta abaixo foi retirado do relatório social anual da mesma empresa do exemplo anterior, e mostra a relação dos valores distribuídos aos segmentos da sociedade. Este é um claro exemplo de uso desnecessário de uma perspectiva em 3D, que não adiciona nenhuma informação, somente “lixo de gráfico.”

Este gráfico sofre de “despenhadeirite”, que é esta representação de altura que aparece em torno da torta, mas que não traz nenhum valor numérico, e só confunde e distrai.

Gráfico retirado do relatório social anual de uma grande empresa, ilustrando a distribuição dos lucros nos segmentos da sociedade. Um exemplo de uso desnecessário de perspectiva em 3D.

Além disso, a representação em perspectiva dos gráficos em 3D distorce o tamanho relativo das partes do gráfico, conferindo maior tamanho às fatias que estão na frente, e relativamente diminuindo as fatias na parte de trás. As pessoas vão pensar que as fatias de baixo são as mais importantes.

No gráfico anterior, as fatias enfatizadas na parte da frente são os lucros repassados ao governo e aos funcionários, e a fatia que está na parte de trás é a dos lucros retidos pela empresa, uma coincidência bastante suspeita.

É um truque comum colocar a fatia que você quer enfatizar na parte de baixo da torta, e aumentar o quanto for possível a altura da torta, e incliná-la o máximo para trás, como no gráfico a seguir. Nele, a distorção das fatias é bastante evidente.

Gráfico retirado do relatório de um órgão governamental europeu. As distorções pela perspectiva são aumentadas com o aumento da altura e da inclinação da torta. Note que o produtor ainda teve o cuidado de adicionar a sombra da torta. Ao confeccionar este gráfico, acredito, já estava sofrendo de insolação.

Caso o produtor ainda não esteja satisfeito com o grau de distorção causada pela perspectiva num gráfico de torta, ele pode colocá-la na vertical e transformar a torta numa roda. As fatias da parte de baixo da roda são apresentadas com um tamanho relativo menor em comparação com as fatias da parte de cima.

Gráfico retirado do relatório anual de uma grande estatal brasileira. Colocar as tortas na vertical e transformá-las em roda agrava ainda mais os problemas do leitor, que além de continuar sendo enganado pela perspectiva, não está familiarizado com este desenho não usual.

Mesmo com todos os efeitos tridimensionais que os computadores nos oferecem ao esforço de um click, parece que essas opções não são mais suficientes para saciar a sede dos produtores que estão mais interessados em valorizar o recipiente do que o conteúdo, ao preço de adicionar mais “lixo de gráfico”. O produtor do gráfico a seguir não ficou satisfeito com a perspectiva em 3D do gráfico de torta, e decidiu adicionar imagens de fotos como textura para cada fatia.

Gráfico retirado do relatório anual da administradora de um porto brasileiro. As fatias ao invés de serem coloridas, são cobertas pela imagem de fotos. Mais um exemplo de preocupação com o estilo que supera a preocupação com a compreensão.

Não é porque os recursos computacionais disponíveis nos permitem criar tais “obras de arte” que devemos considerar que elas são as melhores opções para levarem ao entendimento, e nem devemos cair na tentação de usá-las nos casos em que não agregam informação. Gráficos mais bonitos não são intrinsecamente melhores. Quase todas as demandas por gráficos são satisfeitas por desenhos simples em duas dimensões, que não são tão chamativos, mas levam o leitor à compreensão.

BARRAS INDIGESTAS - CASO 7

O gráfico seguinte é da mesma empresa do exemplo anterior, mas de um relatório anual anterior. Além de apresentar o mesmo problema que foi descrito anteriormente, este gráfico apresenta outro. O gráfico mostra os valores dos ganhos anuais por ação de três anos consecutivos, representados por linhas, que juntas formam um desenho que lembra uma auto-estrada; a linha do meio é tracejada, lembrando a faixa que permite ultrapassagens nas estradas.

Este é um exemplo de como a preocupação com o estilo pode superar a preocupação com a compreensão. Embora realmente seja uma idéia muito criativa fazer um gráfico em forma de auto-estrada no relatório anual de uma empresa automobilística, o problema é que a linha tracejada dá um peso visual menor para o valor da linha do meio, diminuindo visualmente a sua importância relativa às outras linhas. Novamente uma escolha muito suspeita, considerando-se que o ano representado no centro foi o que teve o pior desempenho.

Gráfico dos ganhos anuais por ação de uma grande empresa automobilística dos EUA, cujas linhas que representam o valor de três anos consecutivos, formam o desenho de uma auto-estrada. Um exemplo de preocupação com o estilo ao invés da compreensão.

BARRAS INDIGESTAS - CASO 6

O próximo gráfico foi tirado do relatório anual de uma tradicional empresa automobilística dos EUA. O interessante deste gráfico é que a evolução dos ganhos por ação é mostrada com o ano mais recente à esquerda e os anos anteriores à direita, uma disposição inversa à nossa noção que a direção de leitura, ou seqüência, se realiza da esquerda para a direita, ou mesmo da nossa intuição de que o tempo deve ser representado passando da esquerda para a direita. Essa disposição é uma escolha bastante suspeita, considerando que a empresa não tem números bons para mostrar, e este gráfico pode fazer parecer que o grande número negativo à esquerda estava no passado, e que hoje a empresa voltou a ter resultados positivos, o que na realidade é exatamente o contrário.

Gráfico dos ganhos por ação do relatório anual de uma grande empresa automobilística dos EUA. Note que a evolução dos ganhos é mostrada com os anos decrescendo da esquerda para a direita, fazendo parecer que os ganhos estão subindo, enquanto na verdade se tornaram bem negativos no último ano.

BARRAS INDIGESTAS - CASO 5

O gráfico de barras a seguir apresenta a evolução do endividamento bruto em bilhões de Reais de uma grande estatal brasileira. As barras são divididas em três partes, mostrando parcelas de tipos diferentes de endividamento, e uma linha no alto de cada barra mostra o valor total para aquele ano. Cada parte de cada barra é separada da seguinte por um espaço, que tem o mesmo tamanho em todas as vezes que aparece.

O problema desse gráfico com barras flutuantes é que os espaços vazios aumentam a altura total da barra e inviabilizam a comparação direta entre cada componente da barra e o total, passando a impressão de que cada parte é menor do que realmente é em comparação ao todo, o que pode ser conveniente num gráfico de endividamento que mostra uma tendência de aumento.

As barras flutuantes impedem o leitor de comparar os valores numéricos pela simples comparação do comprimento de cada barra, que é justamente uma das principais vantagens desse tipo de gráfico.

Gráfico da evolução do endividamento bruto em bilhões de reais, retirado do relatório anual de uma grande estatal brasileira. O uso de barras flutuantes impede a comparação entre as partes e o total.

BARRAS INDIGESTAS - CASO 4

O gráfico abaixo, do relatório anual de uma grande empresa de entretenimento dos EUA, mostra a evolução das despesas de capital de um determinado departamento. Cada barra representa o valor das despesas de dois setores, e por isso elas são divididas em duas partes.

As barras são circundadas por uma moldura, com espessura considerável. Então o leitor se pergunta: quem fez o gráfico espera que eu leia o valor da barra incluindo a espessura da moldura, ou sem ela? De acordo com a escala, a espessura da moldura é equivalente a US$ 50 milhões, ou pouco mais de 4% do limite da escala. Uma quantia considerável para investidores e analistas de mercado. Mais um exemplo de “lixo de gráfico.”

Gráfico das despesas de capital de um setor de uma grande empresa de entretenimento dos EUA. O uso de uma moldura em torno das barras confunde o leitor.

BARRAS INDIGESTAS - CASO 3

Outro tipo de gráfico para o qual devemos estar atentos são aqueles que apresentam duas escalas no mesmo gráfico, ilustrando duas variáveis diferentes. Quando estas duas variáveis podem ser comparadas, como quando denotam a mesma grandeza ou unidade de medida, naturalmente tendemos a comparar as curvas ou barras, mas se elas estão em escalas diferentes, essa comparação será enganosa.

O gráfico abaixo mostra a evolução da quantidade de lixo reciclado por uma grande empresa brasileira, e publicado em seu relatório social anual. O eixo da esquerda e as barras ilustram a quantidade de lixo reciclado em toneladas, e o eixo da direita ilustra a porcentagem do total do lixo que é reciclado; ambas as escalas são de base não zero. Isso faz parecer que a quantidade de lixo reciclado aumentou em 400% entre 2004 e 2006, quando na verdade aumentou de menos de 7.000 toneladas para menos de 10.000, um aumento de menos da metade. A outra escala faz parecer que a porcentagem reciclada aumentou em 1/3 do valor anterior, quando na verdade aumentou 1/16 avos.

O problema quando se colocam essas duas medidas relacionadas entre si no mesmo gráfico, em escalas de base não zero, é que as duas escalas estão distorcidas em proporções diferentes. Assim a desinformação se estabelece tanto na comparação entre os anos da mesma variável, quanto entre as duas variáveis. Portanto, escalas mistas é outro item com que se deve tomar cuidado em gráficos e diagramas. A não ser que você seja muito vivo em estatística para notar que existem duas escalas diferentes para o mesmo espaço gráfico, poderá ser enganado.

Gráfico do relatório social anual de uma grande empresa brasileira, mostrando a evolução da reciclagem do seu lixo. A escala da esquerda é da quantidade de lixo reciclado, e a escala da direita mostra a porcentagem em relação ao total de lixo. Ambas as escalas são de base não-zero.

RELATÓRIOS ANUAIS E GRÁFICOS RUINS

Os relatórios anuais de empresas são divulgados para exibir o seu desempenho econômico e financeiro, para investidores e analistas de mercado. Recentemente também estão divulgando os relatórios sociais, nos quais são descritas as ações da empresa para a melhoria da comunidade e preservação do meio-ambiente. A maioria apresenta um estilo sofisticado e colorido, com muitas fotos de setores das fábricas, produtos, funcionários sorridentes, e grupos de diretores em ternos caros e sorrisos confiantes; mas poucos se preocupam em ser ferramentas eficazes de comunicação com sócios, acionistas, e analistas de mercado.

Esses documentos geralmente seguem o mesmo estilo de apresentação de números e gráficos ao longo de todo o relatório, embora a maioria das empresas não mantenha o mesmo estilo entre os relatórios de um ano e outro, forçando os seus leitores a se adaptarem a um novo modo de apresentar as informações a cada ano. São poucas as empresas que definem um estilo visual e o mantêm, apresentando uma coerência; a maioria parece que contrata um projetista de relatório diferente a cada ano, que decide projetar o relatório da maneira que acredita ser a mais adequada.

Estes relatórios corporativos, assim como relatórios governamentais que também serão usados como exemplos aqui, estão cheios de números e gráficos, que não por acaso são de grande interesse para o próprio produtor da informação. Certamente estes relatórios se encaixam na categoria em que o produtor da informação tem grande interesse nos resultados. Só isso já é o suficiente para atribuirmos uma boa dose de desconfiança aos seus números e gráficos, possíveis portadores de distorções e apresentações tendenciosas. Especialmente se a empresa em questão não tem bons números para mostrar, e está ávida para passar uma boa imagem, ou o governo quer justificar um aumento de impostos ou exagerar os progressos realizados.

É importante ressaltar que a precisão, a clareza e a coerência da representação visual dos dados é que estão sendo avaliados aqui, e não o estilo ou a aparência dos gráficos. Certamente muitos gráficos que têm uma representação visual correta poderiam tornar-se mais atrativos ou com uma leitura mais fácil e agradável caso adotassem outras estratégias de desenho, como as recomendadas por Tufte, mas isto não tira o seu mérito por informar corretamente e honestamente o leitor.

CUIDADOS AO PRODUZIR GRÁFICOS - PARTE 7 - USO DE GRÁFICOS 3D

Os gráficos em três dimensões são extremamente fáceis de elaborar no computador; tão fáceis quanto qualquer outro gráfico em duas meras dimensões. Então porque continuar usando os tradicionais e sem graça gráficos em 2D, se podemos usar gráficos em 3D que parecem muito mais legais e passam uma impressão de modernidade e sofisticação? Simples, porque para a grande maioria dos gráficos, não é necessário o uso de três dimensões, e o seu uso só adiciona complexidade e confunde o leitor. Use gráficos em 3D somente se a terceira dimensão adicionar alguma informação.

Como Wurman [WURMAN, Richard Saul. Ansiedade de Informação: Como transformar informação em compreensão. São Paulo: Cultura Editores Associados, 1991, pág. 301] descreve: “A possibilidade de os gráficos mostrarem profundidade cria mais confusão quando esta profundidade não tem valor numérico. Isso acontece tanto em gráficos circulares, como de barras, e bem como em mapas geográficos. Espera-se que você olhe o plano ou a profundidade? Isso serve apenas para confundir a sua percepção da informação.”

E Jones [JONES, Gerald Everett. How to Lie with Charts: Second Edition. Santa Monica: La Puerta Productions, 2007, pág. XVII] é ainda mais enfático ao criticar os gráficos em 3D: “Quando você precisar escolher um tipo de gráfico no PowerPoint, se você quiser enganar e distorcer, escolha tortas ou barras dimensionais. É virtualmente impossível fazer gráficos 3D que não dão a impressão errada.”

Os gráficos em 3D também sofrem do problema que Wurman chama de “despenhadeirite”, que é essa profundidade adicionada aos gráficos, que na maioria das vezes parecem como despenhadeiros circundando-os, como no exemplo acima. São ainda mais graves quando aparecem em mapas 3D, pois passam a impressão de um verdadeiro despenhadeiro, que poderia ter muitos quilômetros de profundidade se medido na mesma escala do mapa.

Gráfico de torta em 3D retirado do prospecto de fundos de investimento de um grande banco brasileiro, mostrando a composição de determinada carteira. Exemplo do uso desnecessário de uma perspectiva em 3D em um gráfico simples, que passa a sofrer de “despenhadeirite.”

Quando você olha o gráfico, sabe que a profundidade não está representando nenhuma informação, mas a sua mente vê essa profundidade e tenta tirar algum significado disso, ou o compara com as outras medidas. O uso de uma dimensão a mais que não traz nenhuma informação numérica só distrai e confunde.

O uso de gráficos 3D quando não são necessários é mais um exemplo de “lixo gráfico”, que mostra uma estupidez gráfica e denigre a imagem do produtor.

Mas os gráficos em 3D podem ser muito úteis quando apropriadamente usados, e não é necessário nem um computador para isso; uma prova que somente ferramentas excelentes não fazem gráficos igualmente excelentes, e a responsabilidade pela sua qualidade ainda recai sobre os ombros do produtor.

O estatístico italiano Luigi Perozzo ficou conhecido na segunda metade do século XIX por seus excelentes diagramas em 3D. Em 1879 ele publicou o seu diagrama mais conhecido, uma representação da pirâmide da idade da Suécia, baseada nos dados estatísticos do censo sueco de 1750 a 1875.

Gráfico em 3 dimensões de Luigi Perozzo, 1880, mostrando a evolução da pirâmide de idades da população da Suécia entre 1750 e 1875. Um exemplo precoce de um bom gráfico em 3 dimensões. [Perozzo, Luigi. Statistica Grafica - Della rappresentazione grafica di una collettività di individui nella successione del tempo, e in particolare dei diagrammi a tre coordinate - Memoria di Luigi Perozzo. Annali di Statistica, Serie 2, Vol. 12, 1880 (Ministero d'Agricoltura, Industria e Commercio, Direzione di Statistica). Imagem disponível em http://www.math.yorku.ca/SCS/Gallery/images/stereo2.jpg]

O gráfico mostra a evolução da pirâmide de idades da população sueca, entre 1750 e 1875. O eixo vertical (altura) representa a quantidade de pessoas, o eixo longitudinal (profundidade) representa as faixas etárias, e o eixo lateral (largura) representa os anos, começando em 1750 e terminando em 1875.

A primeira linha no eixo de idades (mais ao fundo) representa os nascidos vivos, e ela se sobressai sobre o resto do gráfico. Podem-se notar dois fatos interessantes com essa linha: o primeiro fato é que a faixa etária seguinte apresenta uma queda expressiva em população, denotando uma alta mortalidade infantil, mas que tende a diminuir com o passar dos anos; o outro fato é a ascensão rápida do número de nascidos a partir de 1850, o que provoca um degrau na pirâmide dos anos seguintes. Ambos os fatos poderiam ser atribuídos à melhoria da qualidade de vida e aos avanços da ciência e da medicina.

CUIDADOS AO PRODUZIR GRÁFICOS - PARTE 6 - GRÁFICOS SOBRE DINHEIRO SÓ FAZEM SENTIDO SE OS VALORES TÊM A MESMA REFERÊNCIA

O valor do dinheiro muda com o tempo, devido à inflação. Como a inflação é quase sempre positiva, o dinheiro tende a desvalorizar com o tempo. Não faz sentido comparar o valor nominal atual e de vinte anos atrás do preço de um quilo de laranja ou de um quilo de carne. No entanto, faz sentido comparar o preço entre as laranjas e a carne hoje, e entre as laranjas e a carne há vinte anos, pois embora sejam produtos diferentes, apresentam a mesma base monetária, o que permite uma comparação de preços.

Um gráfico que apresenta os valores nominais dos preços no tempo apresenta além da variação da medida (o preço), uma variação no desenho (preços com valores reais diferentes). A escala vertical efetivamente muda, pois o valor do dinheiro muda com o tempo, distorcendo o gráfico. Então, o único modo de pensar claramente sobre dinheiro no tempo é fazer comparações usando unidades monetárias ajustadas pela inflação. Ajuste os valores do passado de acordo com a inflação do período, e assim você saberá que está apresentando os preços em valores reais, e não nominais.

Um exemplo que está constantemente nos noticiários é o preço do barril de petróleo. Os jornalistas estão a todo o momento anunciando, com um semblante de preocupação, a quebra de novos recordes no preço do barril de petróleo. Considerando que esse preço é cotado em dólares americanos, e há inflação nos Estados Unidos, então é de se esperar que com o passar do tempo o preço nominal seja reajustado e chegue a patamares inéditos, no entanto, sem implicar necessariamente num aumento real.

O gráfico a seguir mostra a variação do preço do barril de petróleo de Janeiro de 2000 a Janeiro de 2005. O observador perceberá uma clara tendência de aumento, e logo concluirá que deverá esperar por um aumento no preço dos combustíveis em breve.

O que pode passar despercebido é que o título do gráfico indica que estes são os valores nominais, e, portanto, sem o ajuste pela inflação. Se este gráfico tiver os valores do passado ajustados pela inflação, eles tornarão-se valores reais, o que geralmente significa valores absolutos maiores. Quanto mais no passado estiver o valor, maior a inflação acumulada no período, e maior será a diferença entre o valor nominal e o real.

O gráfico com os valores reais tenderá a ser mais plano, e a tendência de subida dos preços ficará menos evidente.

Gráfico retirado do relatório anual de uma grande estatal brasileira, mostrando a variação do preço nominal em dólares americanos por barril do petróleo entre Janeiro de 2000 e Janeiro de 2005, de acordo com três cotações. Valores de dinheiro no tempo não deflacionados causam uma variação no desenho, pois o eixo vertical muda.

Tufte [TUFTE, Edward Rolf, The Visual Display of Quantitative Information. Cheshire: Graphics Press, 2007, pág. 68] sugere o seguinte princípio para gráficos sobre dinheiro: “Em visualizações de dinheiro no tempo, unidades de medida monetárias deflacionadas e padronizadas são quase sempre melhores que unidades nominais.”

Os gráficos orçamentários dos governos também devem considerar os efeitos da inflação, assim como uma segunda fonte de distorção: a variação da população. As medidas orçamentárias dos governos, como a arrecadação de impostos, as despesas com serviços públicos, ou os investimentos em determinado setor, são diretamente proporcionais à população que paga impostos, utiliza os serviços públicos ou indica um crescimento que requer novos investimentos.

Do mesmo modo que a comparação entre valores monetários em tempos diferentes requer a utilização de uma unidade padronizada de medida (como por exemplo, os preços deflacionados ou reais), a comparação de receitas e despesas do governo só fazem sentido quando reduzidas a uma unidade padronizada de medida que leve em consideração a população considerada. Em gráficos governamentais, faz muito mais sentido pensar em termos de unidades monetárias reais per capita.

Os gráficos de orçamentos e gastos governamentais geralmente dão a impressão de estarem subindo rapidamente, o que serve de material para muitas reportagens sensacionalistas e críticas ao governo. Entretanto é de se esperar que os valores de arrecadação e gastos dos governos constantemente cheguem a valores nominais inéditos, tanto pelo efeito da inflação, quanto pelo aumento da população. Este efeito só não ocorrerá em localidades com deflação, ou decréscimo populacional.

Assim, enquanto gráficos em valores nominais podem indicar um aumento de orçamento ou despesas, quando normalizados pela inflação e pelo aumento da população, podem indicar até uma queda.

Gráfico de evolução da receita do Governo do Estado de São Paulo entre 2000 e 2006, que indica um crescimento estabilizado. Note que os valores apresentados são nominais. Se as medidas deste gráfico fossem padronizadas em unidades monetárias reais per capita, poderiam indicar um nível constante ou até mesmo um decréscimo de receita. [Gráfico disponível em http://www.planejamento.sp.gov.br/PlanOrca/orca.asp]

A aplicação da aritmética faz possível levar em consideração a população e a inflação. Computar gastos em unidades monetárias reais per capita geralmente revela uma situação bem diferente e mais precisa do que os gráficos de medidas não padronizadas.

CUIDADOS AO PRODUZIR GRÁFICOS - PARTE 5 - GRÁFICOS EMPILHADOS PODEM ESCONDER INFORMAÇÕES

Gráficos de áreas ou barras empilhadas são uma boa maneira de aglomerar vários conjuntos de dados numa mesma área de desenho. Porém eles também têm potencial para enganos e mentiras.

A primeira pergunta que vem é: as barras ou áreas estão colocadas uma sobre as outras, ou uma atrás das outras? Jones [JONES, Gerald Everett. How to Lie with Charts: Second Edition. Santa Monica: La Puerta Productions, 2007, pág. 40]: explica bem este problema: “As áreas ou barras estão empilhadas verticalmente – como tijolos e argamassa – ou estão em camadas uma em cima do outra – como desenhos em folhas transparentes separadas, e cada nova área começando na mesma linha horizontal na parte de baixo do gráfico? Se as áreas estão realmente empilhadas, somente os dados de baixo terão uma linha de base plana. Cada nova área terá o topo da área precedente como a sua linha de base, e qualquer flutuação nesta linha irá distorcer os altos e baixos da área seguinte.”

Gráfico de barras empilhadas (à esquerda), e de áreas empilhadas (à direita), retirados do relatório de um órgão governamental europeu. Note que somente o primeiro conjunto de dados, aquele cujas barras ou áreas se iniciam no eixo horizontal, é que apresentam a mesma linha de base.

Se os dados estiverem realmente empilhados como tijolos, significa que a o conjunto de dados seguinte usa como base a parte superior do conjunto de dados anterior. Portanto, é claro que quanto maior a variação do dado que é colocado na parte de baixo, maior será o efeito de flutuação do dado que está em cima. Este efeito pode ser minimizado pelo produtor bem intencionado, que coloca perto da base o conjunto de dados com menor variação, e, portanto que causará menos flutuação aos conjuntos acima. Mas caso o produtor queira gerar confusão ou confundir o leitor, poderá colocar a variável com maior flutuação na parte de baixo, e transformar a leitura do gráfico em uma árdua tarefa.

Já os gráficos que empilham os conjuntos de dados em camadas não apresentam este problema, pois todos os conjuntos de dados começam na mesma base, o eixo horizontal. No entanto, só funcionam bem se o conjunto de dados à frente apresenta sempre valores menores do que os conjuntos de dados atrás; caso em contrário, partes dos conjuntos de dados de trás ficarão escondidos, o que pode até ser conveniente para um produtor desonesto.

O gráfico a seguir é um bom exemplo deste tipo de representação em camadas. A anterior é a de nascimentos, a camada seguinte é a de óbitos, e a camada mais frontal é a de casamentos. Esta ordem foi uma escolha lógica, pois como geralmente uma população apresenta crescimento, o número de nascimentos será maior que o de óbitos. Já o número de casamentos implica a consideração de duas pessoas, o que quase sempre irá significar um número menor que o de nascimentos e óbitos (as pessoas se casam em pares, mas nascem e morrem individualmente).

Gráfico com as estatísticas de nascimentos, óbitos e casamentos em 1916, a cada mês. Um bom exemplo de gráfico empilhado em camadas, apesar da representação visual pesada gerada pelas hachuras. Além disso, o desenho não é neutro ao usar uma corrente e cadeados para demarcar a linha dos casamentos, e poderia gerar polêmica. [Annuario de Estatística Demographo-Sanitaria de 1915-1916, pelo Dr. Sampaio Vianna, Imprensa Nacional, Rio de Janeiro, 1926. Figura entre as páginas 30 e 31. Documento disponível em http://memoria.nemesis.org.br]

CUIDADOS AO PRODUZIR GRÁFICOS - PARTE 4 - MUDANÇAS NA ESCALA HORIZONTAL OU NA LARGURA AFETAM A PERCEPÇÃO

A escolha da largura de um gráfico afeta a percepção da evidência dos dados. Gráficos estreitos e altos ajudam a enfatizar as variações. Gráficos largos ajudam a amenizar as variações. O produtor pode escolher a razão entre altura e largura que melhor conduzir ao significado que ele quer passar.

Se o produtor tem um gráfico que mostra muitas flutuações, ou tendências indesejadas de subida ou queda, basta alongar o gráfico para amenizar tais evidências visuais. Caso queira enfatizar tais variações, basta tornar o gráfico alto e estreito.

Um efeito parecido pode ser conseguido com um outro truque mais sutil, que é mudar o valor da escala no eixo horizontal, sem nenhum razão aparente. O leitor incauto não perceberá as escalas que variam de valor, e será conduzido somente pela evidência visual do gráfico.

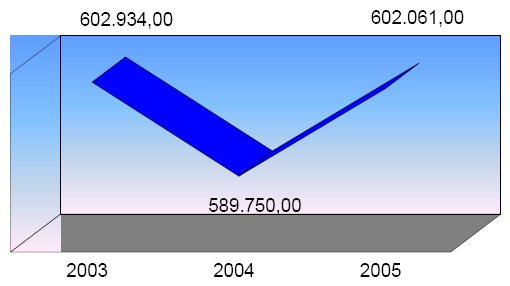
O gráfico a seguir usa este truque de uma maneira bem leve. O tempo entre a primeira barra e a terceira barra equivale a dez anos; logo, o leitor supõe que a barra do meio, colocada igualmente espaçada entre as duas outras barras, representa um valor do meio, ou seja, de cinco anos; no entanto, a barra do meio representa seis anos. Neste caso, para passar uma evidência visual correta, esta barra deveria ser colocada ligeiramente para a direita, mais próximo à barra dos dez anos. O observador que não se atenta a essa mudança, tem a impressão de uma tendência de queda menor do que realmente é.

Gráfico retirado do relatório anual de uma grande companhia automobilística japonesa. As distâncias na escala horizontal não coincidem com os valores de tempo, e passam uma impressão de variação distorcida ao leitor.

O gráfico a seguir é um ótimo exemplo de como não fazer um gráfico, ou como cometer vários erros de representação visual em alguns centímetros quadrados.

Um dos seus problemas é bem comum, que é a escala que não começa no zero, o que dá uma impressão exagerada na taxa de mudança dos valores. Enquanto parece que o valor de mercado das empresas americanas despencou de um pico a zero (isso mesmo, o gráfico dá a impressão que as empresas não valem mais nada, uma vez que o final da linha de evolução encosta-se ao eixo horizontal), na verdade elas desvalorizaram cerca de 17% (de 17,054 para 14,082 trilhões de dólares).

Mas o problema mais grave está na escala horizontal, que divide o tempo analisado em três períodos: março a outubro, outubro a dezembro, e dezembro a março. Entretanto, as divisões não apresentam tamanhos iguais, e nem denotam o mesmo período de tempo.

A primeira divisão representa 6 meses (abril, maio, junho, julho, agosto e setembro), e tem 80% do tamanho da segunda divisão. A segunda divisão representa apenas 1 mês (novembro) e é maior que a primeira, que representa 6 meses, e ligeiramente maior que a terceira, que representa 2 meses (janeiro e fevereiro).

Caso este gráfico estivesse representado com um escala de tempo coerente e espacialmente proporcional ao tempo representado em cada período, poder-se-ia notar uma tendência de queda muito mais acentuada que a mostrada por este, o que corroboraria o ponto de vista da reportagem, que tenta chamar a atenção para a crise da bolsa de valores americana.

Este é provavelmente um caso em que o desenho de gráfico ruim atuou contra os interesses do seu produtor, amenizando, ou invés de exagerar, as evidências da notícia. Nestes casos pode-se afirmar, com certa dose de confiança, que o produtor sofreu de desinformação, falta de atenção ou ignorância.

Gráfico com problemas nas escalas vertical e horizontal. Na medida do tempo, não há coerência ao longo do eixo sobre a proporcionalidade entre a medida usada no desenho e o tempo representado. [O Estado de São Paulo, 23 de março de 2008, pág. B4. Imagem digitalizada a partir do original]

Mas o uso de mudanças nas escalas não é intrinsecamente incorreto, e nem sempre é desonesto. Desde que a mudança na escala seja claramente indicada ao leitor, e este esteja ciente de que a representação visual pode estar distorcida, não há problemas.

A seguir, no eixo vertical da direita (que indica porcentagens), há uma indicação de descontinuidade na escala. O símbolo de descontinuidade (≈) é uma solução muito mais honesta do que simplesmente começar a escala num valor diferente de zero.

Gráfico retirado do relatório anual de uma empresa automobilística japonesa, com uma indicação de descontinuidade na escala do eixo vertical direito. Um exemplo de uso honesto de escala descontínua.

O próximo exemplo faz um uso mais extensivo das descontinuidades, e ainda assim de forma honesta. A escala horizontal apresenta o símbolo de descontinuidade para enfatizar ao leitor que há uma diferença de escala entre os anos de “90” e “02”, que logo é seguido por anos consecutivos. Esta indicação é repetida na linha de evolução na área do gráfico, reforçando a indicação de mudança de escala. O mesmo acontece com a escala vertical, que apresenta duas linhas em paralelo que vão serpenteando através das barras para indicar uma descontinuidade na escala, que corretamente começou no zero. Um produtor desonesto teria usado uma escala de base não zero, ou mesmo esta descontinuidade, sem qualquer preocupação em indicar ou chamar a atenção sobre isto.

Gráfico retirado do relatório anual de uma empresa automobilística japonesa, com indicações de escalas descontínuas em ambos os eixos. Escalas descontínuas podem ser usadas honestamente, desde que indicadas ao leitor.

Usar escalas descontínuas sem evidenciar isto ao leitor é desonesto, pois fornece uma representação visual distorcida em relação ao que o leitor está esperando do desenho do gráfico.

Mas mesmo o uso de escalas descontínuas indicadas ao leitor deve ser usado com cuidado, pois mesmo sendo tecnicamente correto e honesto, continua distorcendo a imagem geral do gráfico e dificultando a análise. O leitor é obrigado a abstrair mentalmente como seria o gráfico se a escala fosse contínua, para ter uma noção mais realista das tendências e variações dos valores. Além disso, as descontinuidades nas escalas geram algumas perguntas incômodas: O que o autor está deixando de fora? O que há na área descontínua que poderia mudar a análise do gráfico? Se a escala fosse contínua o gráfico transmitiria outra mensagem?